Smith Kaart Oefening 2

Opgave

Hoe gebruik je een Smith kaart om een antenne van 80 Ohm aan te passen aan een coax van 50 Ohm voor een frequentie van 300 MHz (\(\lambda\)= 50 cm)?

Oplossing 1: Bijplaatsen van een capaciteit in serie

We plaatsen \(z= \frac{Z_L}{Z_0}=1.6\) op de Smith kaart (rode dotje) en we zoeken waar we de r=1 cirkel snijden in het bovenste deel van de Smith kaart (groene dotje).

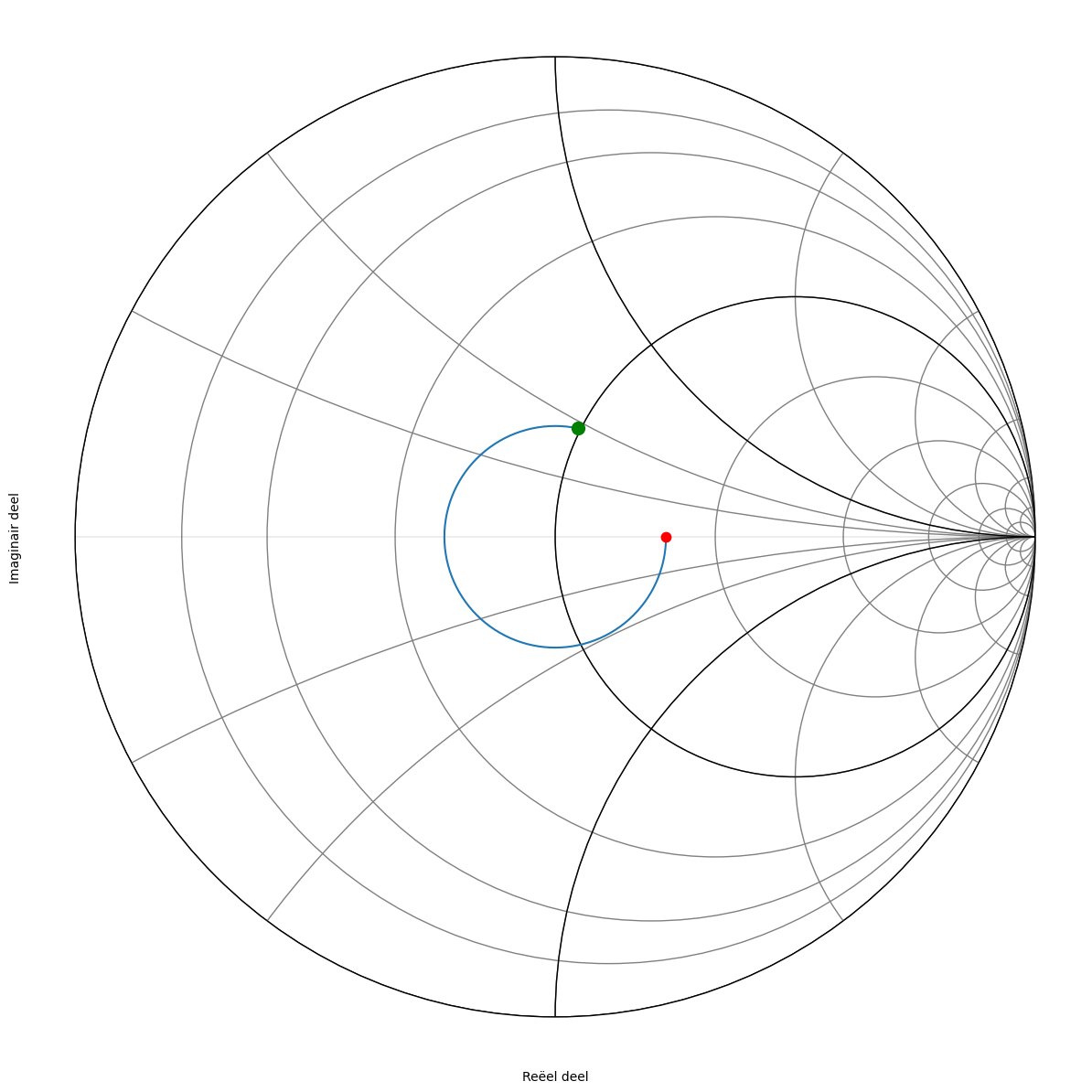
Fig. 140 Smith kaart van de eerste oplossing.

Als we van de aanpassing (groene dot) naar de belasting gaan (rode dot), draaien we in tegenwijzerzin over een afstand van \(283^o\). Dit geeft een afstand van \(\frac{283}{360}\frac{\lambda}{2}\)=0.393 \(\lambda\) = 19.65cm. (\(\lambda\)= 50 cm is gegeven)

De nieuwe z = 1 + j 0.47. Daaruit volgt dat Z = 50 Ohm + j 23.68 Ohm (zie Table 1). Het complexe deel van deze impedantie kunnen we compenseren door een condensator met impedantie van ongeveer - j 23.68 Ohm toe te voegen. Als we het helemaal juist willen hebben kunnen we in de array van de lijnimpedantie (zie Table 1) juist gaan kijken waar het reele deel 50 Ohm wordt en wat we dan als complex deel over houden.

\[ \frac{1}{j \omega C}= - j 23.68 \Omega\]

Als we vervolgens \(\omega\) invullen, wetende dat de freqentie f=300 MHz:

\[ \omega= 2 \pi \cdot 300\times 10^6 \]

\[ C= 22.4 pF \]

hoek    impedantie (Ohm)     lengte coax (cm)
 280  Z= 48.65+23.35j Ohm     lengte=19.44 cm
 281  Z= 49.04+23.47j Ohm     lengte=19.51 cm
 282  Z= 49.45+23.58j Ohm     lengte=19.58 cm
 283  Z= 49.86+23.68j Ohm     lengte=19.65 cm
 284  Z= 50.27+23.78j Ohm     lengte=19.72 cm

Overzicht van de bekomen impedantie als funktie van de hoek op de Smith kaart. De laatste kolom geeft de nodige lengte van de coax

De optimale condensatorwaarde in serie wordt dus 22.4 pF en de nodige lengte van de coax tussen de antenne en de aanpassing is 19.65 cm

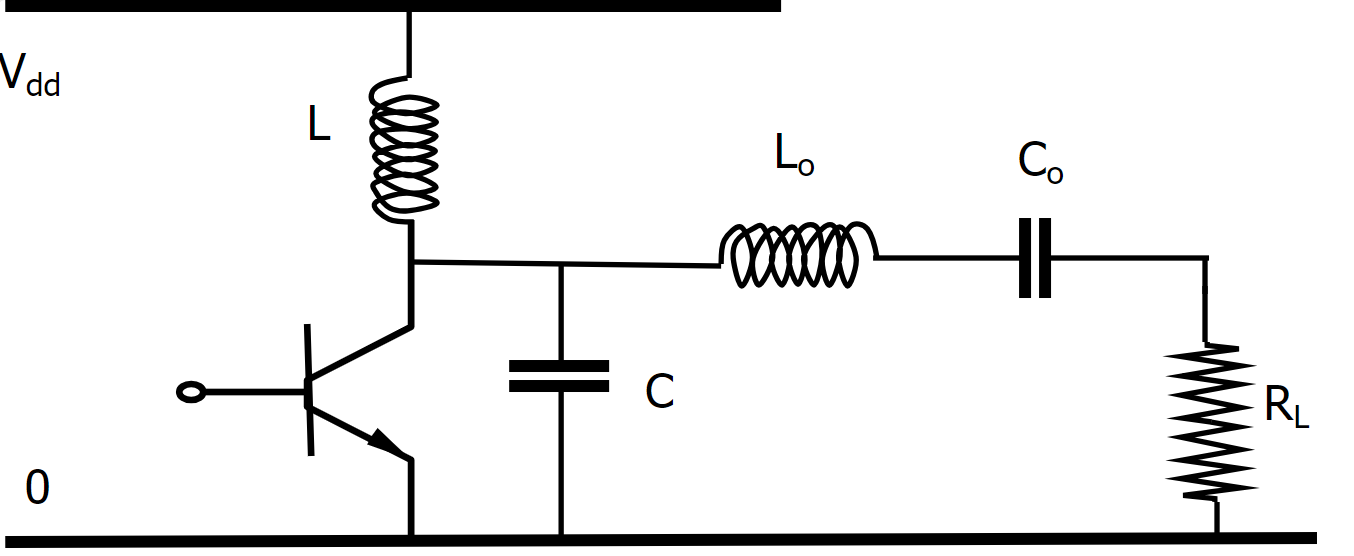
Het schema dat we nodig hebben om deze eerst oplossing te realiseren wordt dus:

Fig. 141 circuit van de eerste oplossing.

Oplossing 2: Bijplaatsen van een inductantie in serie

We plaatsen \(\frac{Z_L}{Z_0}=1.6\) op de Smith kaart en we zoeken waar we de r=1 cirkel snijden in het onderste deel van de kaart.

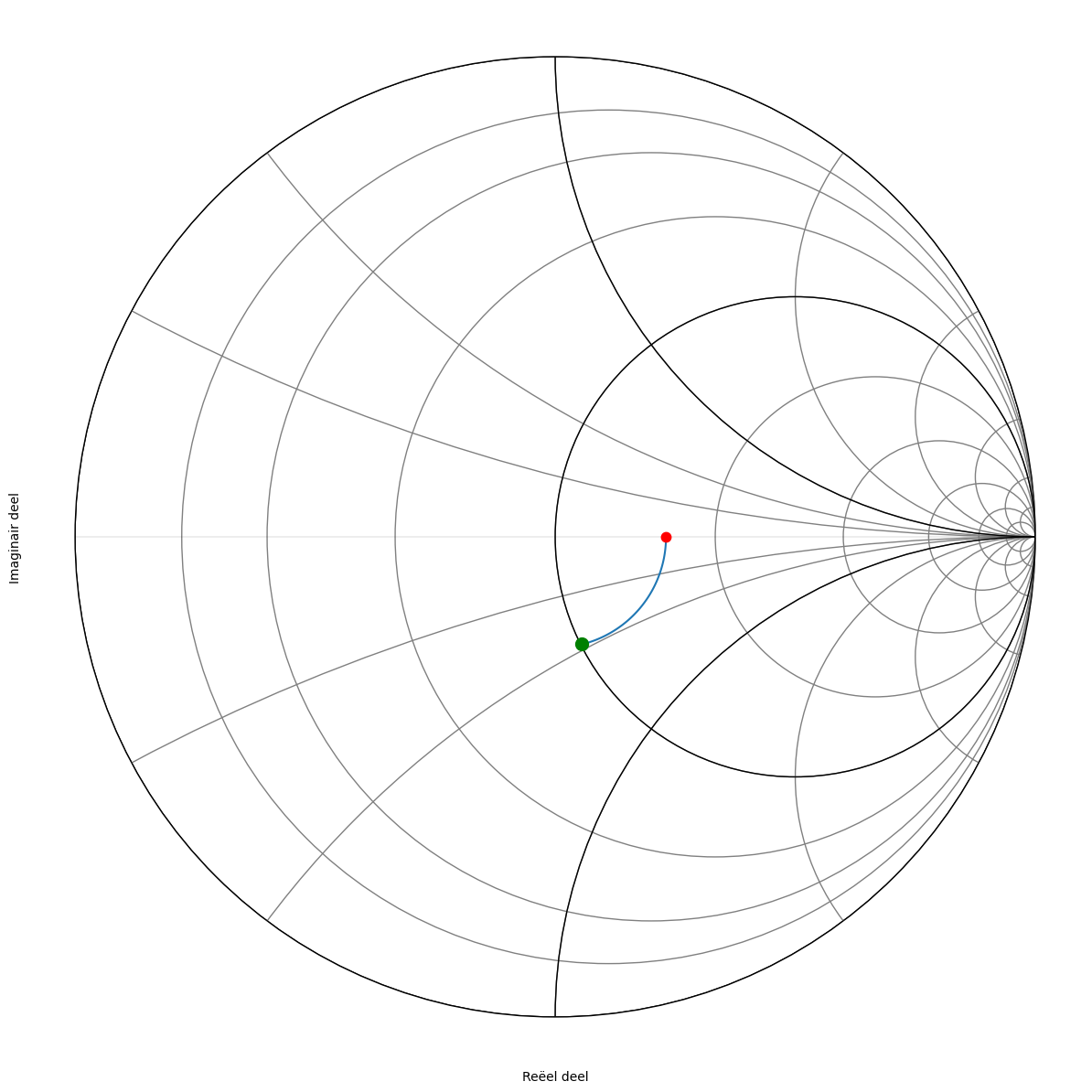
Fig. 142 Smith kaart van de tweede oplossing.

We zoomen vervolgens in op het deel van de cirkel die de eenheidscirkel snijdt.

hoek    impedantie (Ohm)     lengte coax (cm)
  75  Z= 50.69-23.87j Ohm     lengte=5.21 cm
  76  Z= 50.27-23.78j Ohm     lengte=5.28 cm
  77  Z= 49.86-23.68j Ohm     lengte=5.35 cm
  78  Z= 49.45-23.58j Ohm     lengte=5.42 cm
  79  Z= 49.04-23.47j Ohm     lengte=5.49 cm

Overzicht van de bekomen impedantie als funktie van de hoek op de Smith kaart. De laatste kolom geeft de nodige lengte van de coax

De nieuwe z = 1 - j 0.47. Daaruit volgt dat Z = 50 Ohm - j 23.68 Ohm. Het complexe deel van deze impedantie kunnen we compenseren door een spoel met impedantie van ongeveer j 23.68 Ohm toe te voegen. Als we het helemaal juist willen hebben kunnen we in de array van zlijn juist gaan kijken waar het reele deel 50 Ohm wordt en wat we dan als complex deel over houden.

\[ j \omega L= j 23.68 \Omega\]

\[ \omega= 2 \pi \cdot 300 \times 10^6 \]

\[ L=12.56 nH \]

Het schema dat we nodig hebben om deze tweede oplossing te realiseren wordt dus:

Fig. 143 circuit van de tweede oplossing.

De optimale inductantiewaarde in serie wordt dus 12.56 nH en de nodige lengte van de coax tussen de antenne en de aanpassing is 5.3 cm

Oplossing 3: Bijplaatsen van een capaciteit in parallel

We plaatsen \(\frac{Z_L}{Z_0}=1.6\) op de Smith kaart en we zoeken waar we de y=1 cirkel snijden in het bovenste deel van de kaart.

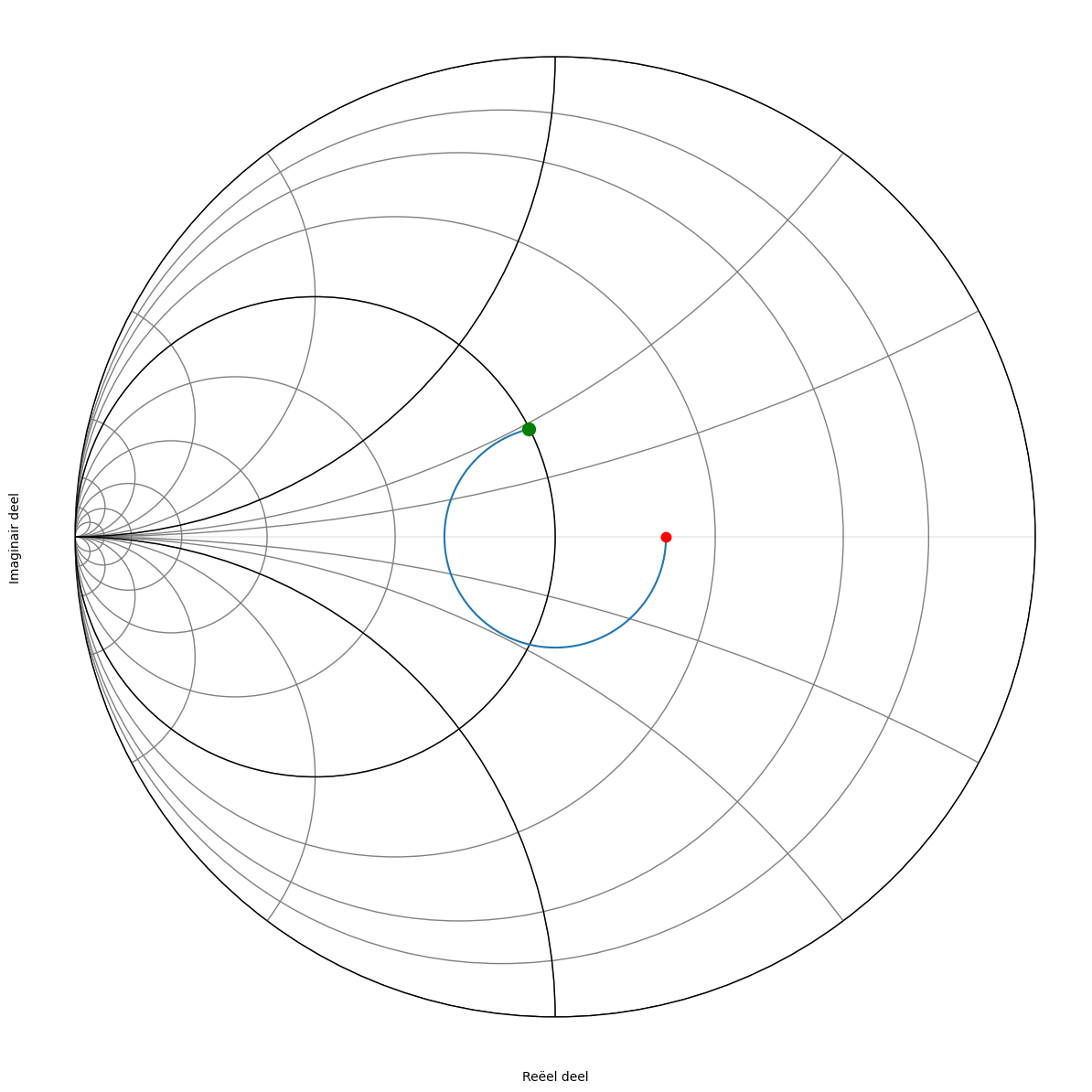
Fig. 144 Smith kaart van de derde oplossing.

Omdat een Smith kaart in admitantie het spiegelbeeld is van een Smith kaart in impedentie, kunnen we ook de kaart spiegelen. We moeten dan wel aan de andere kant van de kaart vertrekken. Dit is weergegeven in figuur 6.

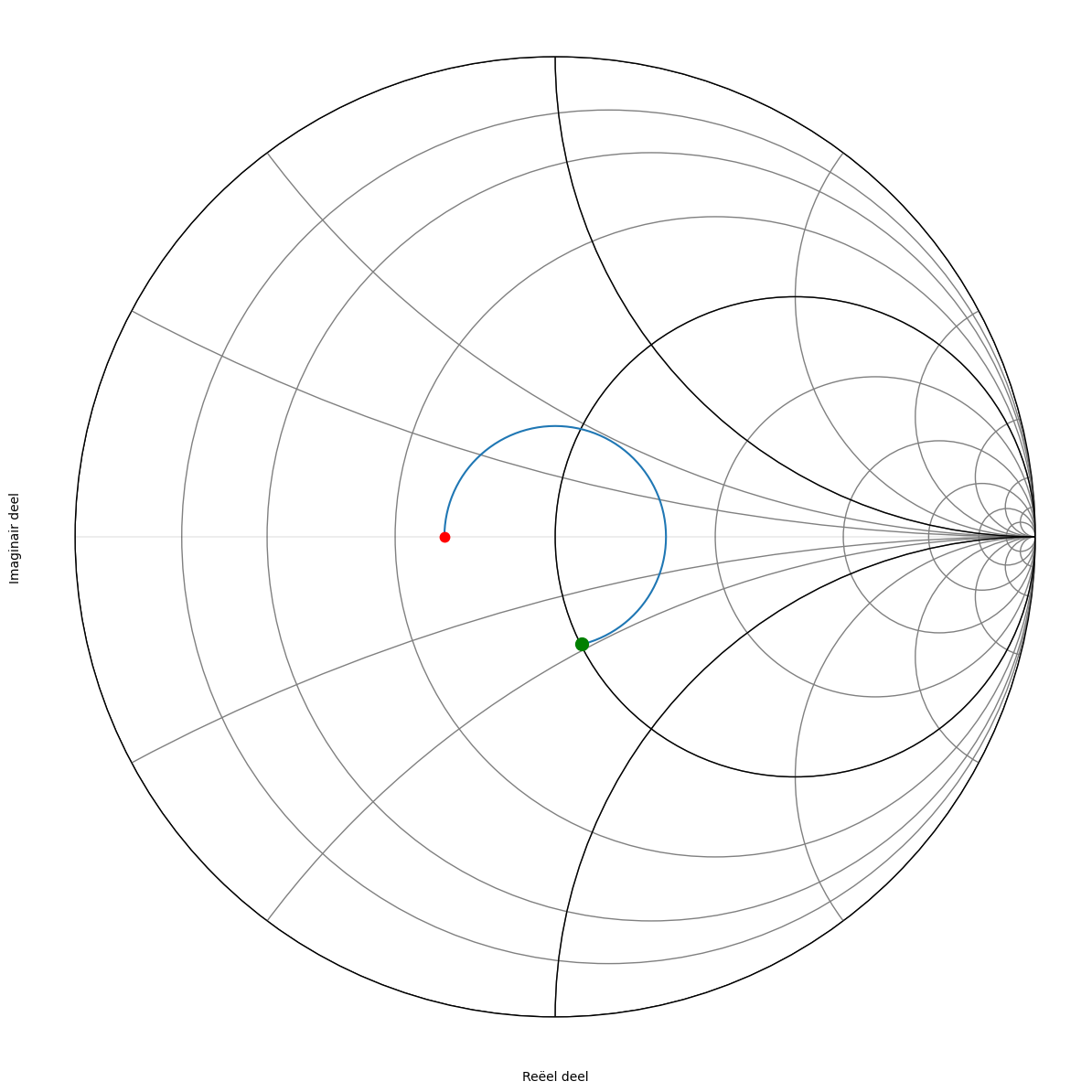
Fig. 145 Smith kaart van de derde oplossing als admittantie.

hoek    admitantie (Siemens)     lengte coax (cm)
 255    Y= 20.28-9.55j mS     lengte=17.71 cm
 256    Y= 20.11-9.51j mS     lengte=17.78 cm
 257    Y= 19.94-9.47j mS     lengte=17.85 cm
 258    Y= 19.78-9.43j mS     lengte=17.92 cm
 259    Y= 19.62-9.39j mS     lengte=17.99 cm

Overzicht van de bekomen admitantie als funktie van de hoek op de Smith kaart. De laatste kolom geeft de nodige lengte van de coax

De optimale condensatorwaarde in parallel wordt dus 5 pF en de nodige lengte van de coax tussen de antenne en de aanpassing is 17.8 cm

\[ j \omega C= 0.00947 j \]

\[ C =\frac{0.00947}{2 \pi \cdot 300 \times 10^6}= 5 pF \]

Het schema dat we nodig hebben om deze derde oplossing te realiseren wordt dus:

Fig. 146 circuit van de derde oplossing.

Oplossing 4: Bijplaatsen van een spoel in parallel

We plaatsen \(\frac{Z_L}{Z_0}=\frac{1}{1.6}\) op de Smith kaart en we zoeken waar we de y=1 cirkel snijden in het bovenste deel van de kaart.

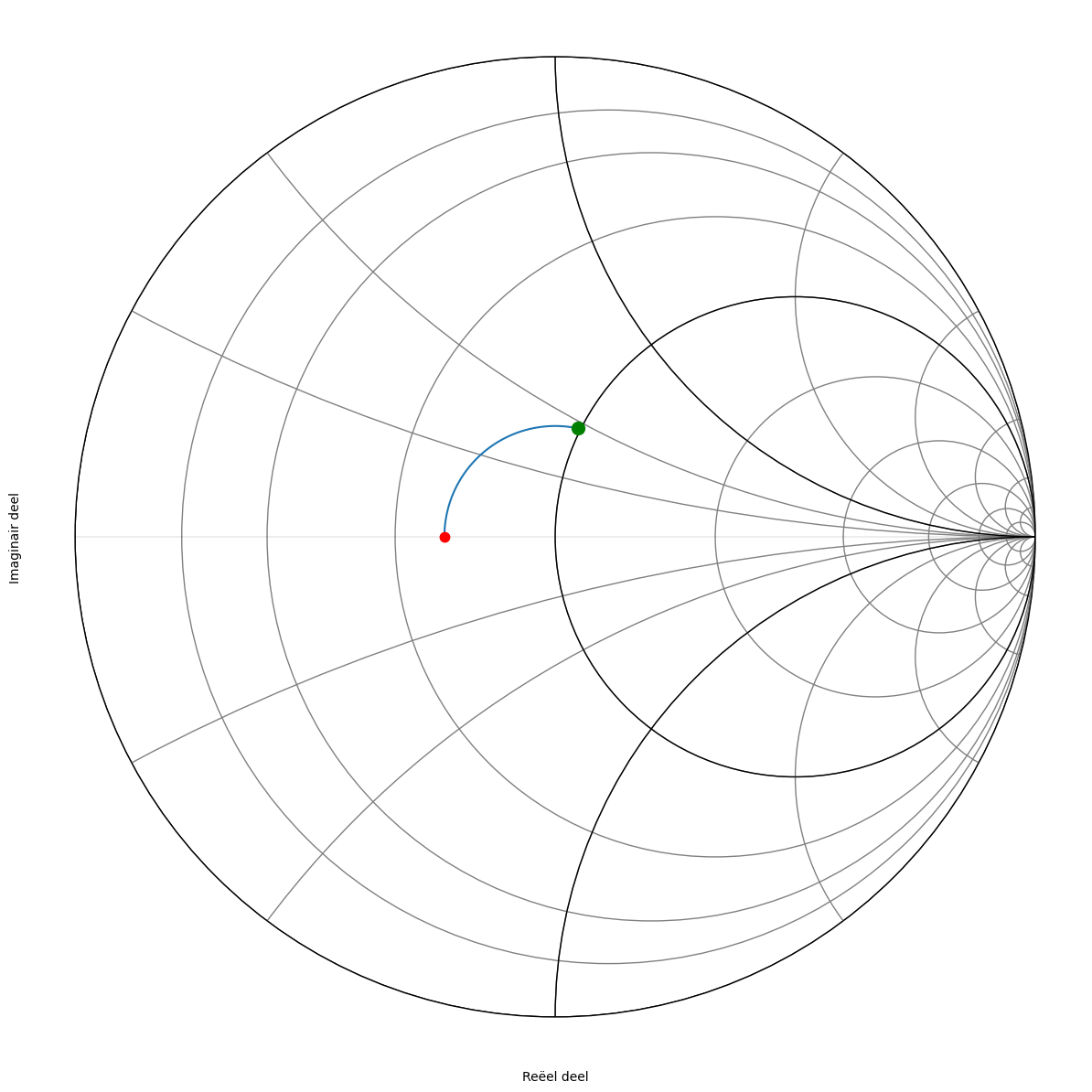
Fig. 147 Smith kaart van de vierde oplossing.

hoek    admitantie (Siemens)     lengte coax (cm)
 100    Y= 19.46+9.34j mS     lengte=6.94 cm
 101    Y= 19.62+9.39j mS     lengte=7.01 cm
 102    Y= 19.78+9.43j mS     lengte=7.08 cm
 103    Y= 19.94+9.47j mS     lengte=7.15 cm
 104    Y= 20.11+9.51j mS     lengte=7.22 cm

Overzicht van de bekomen admitantie als funktie van de hoek op de Smith kaart. De laatste kolom geeft de nodige lengte van de coax

\[ \frac{1}{j \omega L}= - 0.00947 j \]

\[ L =\frac{1}{0.00947\cdot 2 \pi \cdot 300 \times 10^6}= 56 nH \]

De optimale inductantiewaarde in parallel wordt dus 56 nH de nodige lengte van de coax tussen de antenne en de aanpassing is 7.2 cm

Het schema dat we nodig hebben om deze vierde oplossing te realiseren wordt dus:

Fig. 148 circuit van de vierde oplossing.

Oplossing 5: Oplossing 3 waarbij de condensator vervangen is door een open transmissielijn

De y = 1 - j 0.47 compenseren we door +j 0.47 vertrekkende vanuit g=0.

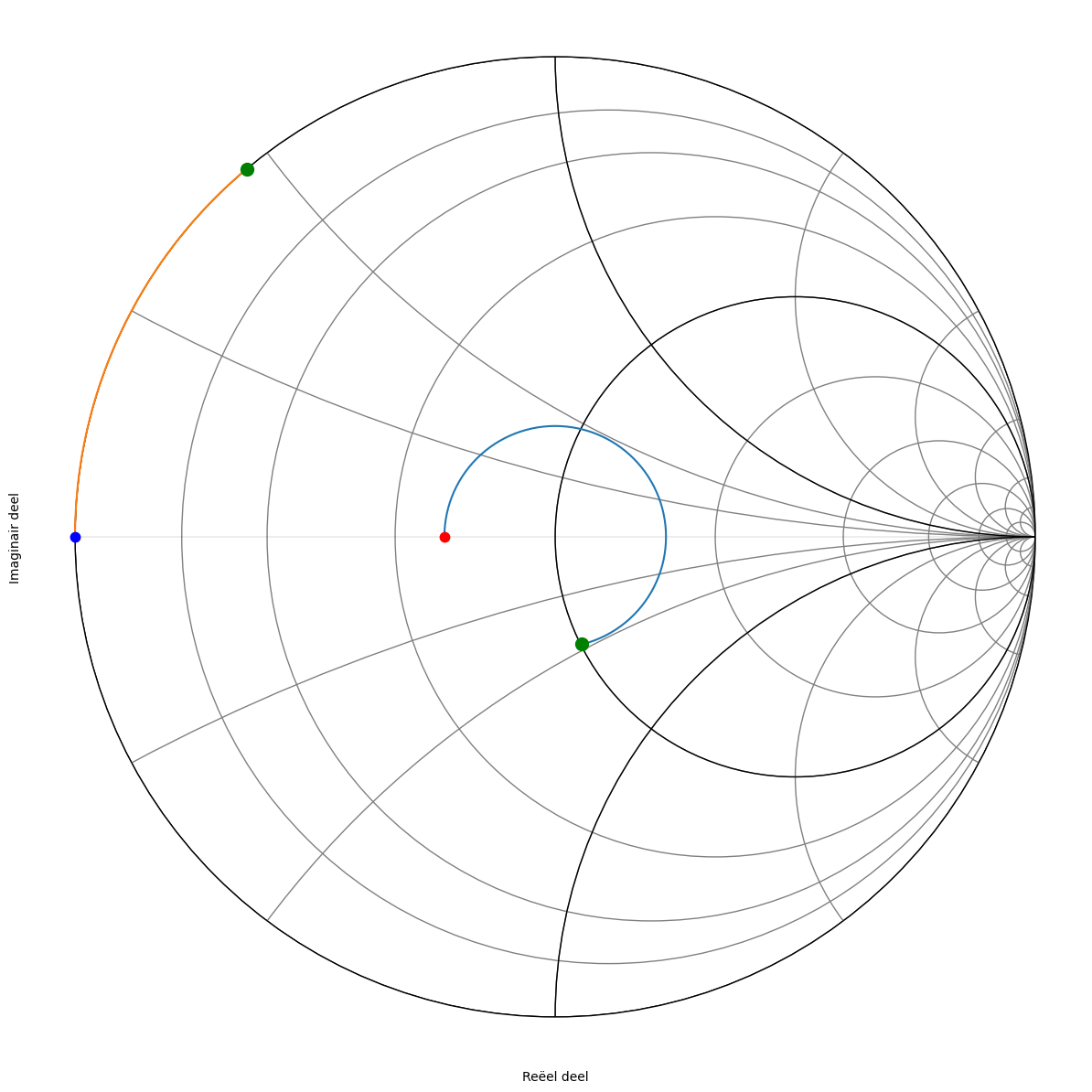
Fig. 149 Smith kaart van de vijfde oplossing.

hoek    admitantie (Siemens)     lengte coax (cm)
 255    Y= 20.28-9.55j mS     lengte=17.71 cm
 256    Y= 20.11-9.51j mS     lengte=17.78 cm
 257    Y= 19.94-9.47j mS     lengte=17.85 cm
 258    Y= 19.78-9.43j mS     lengte=17.92 cm
 259    Y= 19.62-9.39j mS     lengte=17.99 cm

Overzicht van de bekomen admitantie als funktie van de hoek op de Smith kaart. De laatste kolom geeft de nodige lengte van de coax

hoek    admitantie (Siemens)     lengte coax (cm)
  50       Y= +9.33j mS     lengte=3.47 cm
  51       Y= +9.54j mS     lengte=3.54 cm
  52       Y= +9.75j mS     lengte=3.61 cm
  53       Y= +9.97j mS     lengte=3.68 cm
  54       Y= +10.19j mS     lengte=3.75 cm

Overzicht van de bekomen admitantie van de open transmissielijn als funktie van de hoek op de Smith kaart. De laatste kolom geeft de nodige lengte van de coax

Hieruit blijkt dat een open transmissielijn met de lengte van \(\frac{51}{360} \frac{\lambda}{2}\) de beste aanpassing geeft.

Het stukje open coax dat we moeten voorzien ter vervanging van de condensator is dus: 3.54 cm

Het schema dat we nodig hebben om deze vijfde oplossing te realiseren wordt dus:

Fig. 150 circuit van de vijfde oplossing.

Oplossing 6: Oplossing 3 waarbij de condensator vervangen is door een kortgesloten transmissielijn

De y = 1 - j 0.47 compenseren we door +j 0.47 vertrekkende vanuit g=\(\infty\)

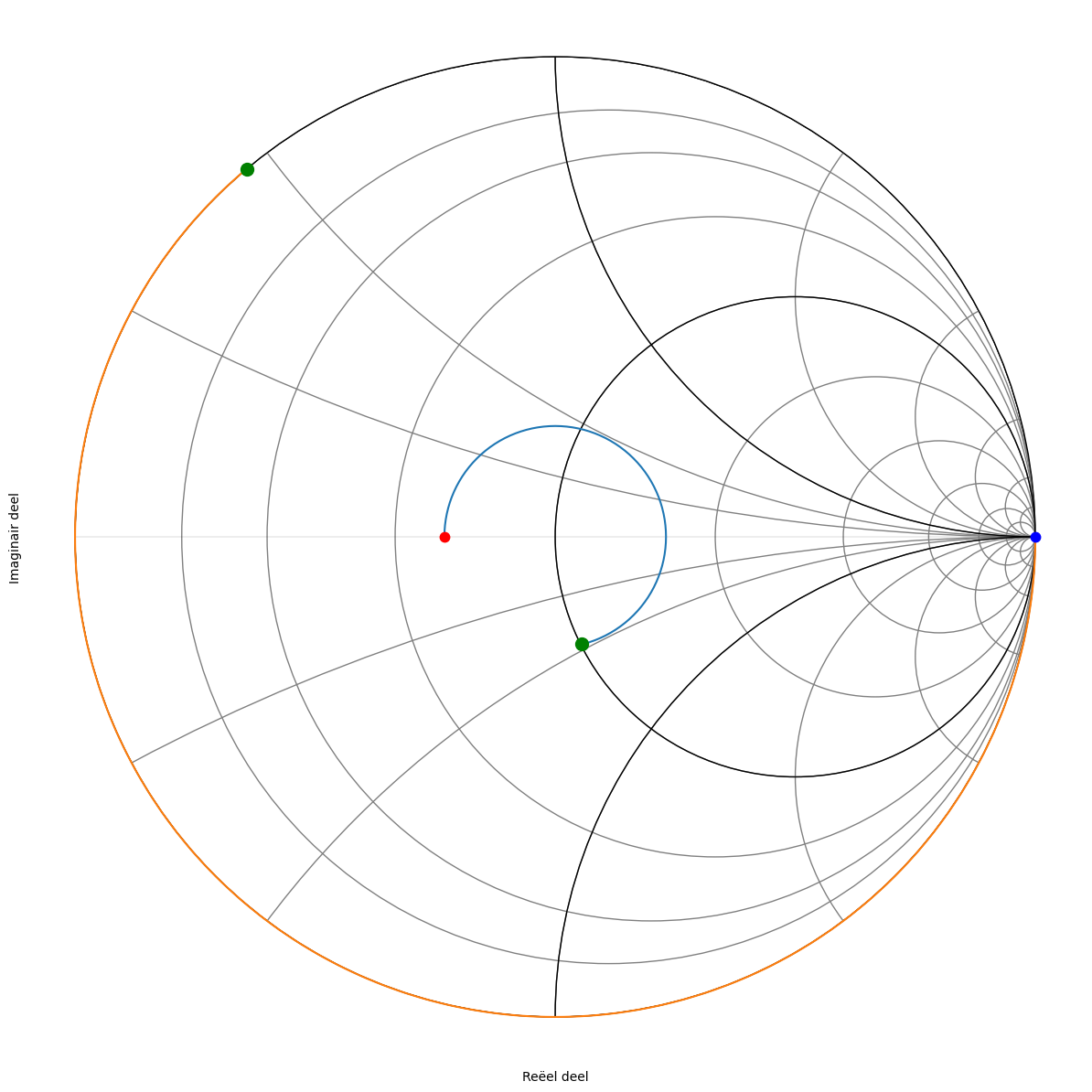
Fig. 151 Smith kaart van de zesde oplossing.

hoek    admitantie (Siemens)     lengte coax (cm)
 255    Y= 20.28-9.55j mS     lengte=17.71 cm
 256    Y= 20.11-9.51j mS     lengte=17.78 cm
 257    Y= 19.94-9.47j mS     lengte=17.85 cm
 258    Y= 19.78-9.43j mS     lengte=17.92 cm
 259    Y= 19.62-9.39j mS     lengte=17.99 cm

Overzicht van de bekomen admitantie als funktie van de hoek op de Smith kaart. De laatste kolom geeft de nodige lengte van de coax

hoek    admitantie (Siemens)     lengte coax (cm)
 230       Y= +9.33j mS     lengte=15.97 cm
 231       Y= +9.54j mS     lengte=16.04 cm
 232       Y= +9.75j mS     lengte=16.11 cm
 233       Y= +9.97j mS     lengte=16.18 cm
 234       Y= +10.19j mS     lengte=16.25 cm

Overzicht van de bekomen admitantie van de kortgesloten transmissielijn als funktie van de hoek op de Smith kaart. De laatste kolom geeft de nodige lengte van de coax

Het stukje kortgesloten coax dat we moeten voorzien ter vervanging van de condensator is dus: 16 cm

Het schema dat we nodig hebben om deze zesde oplossing te realiseren wordt dus:

Fig. 152 circuit van de zesde oplossing.

Oplossing 7: Oplossing 4 waarbij het spoel vervangen is door een open transmissielijn

De y = 1 + j 0.47 compenseren we door -j 0.47 vertrekkende vanuit g=0.

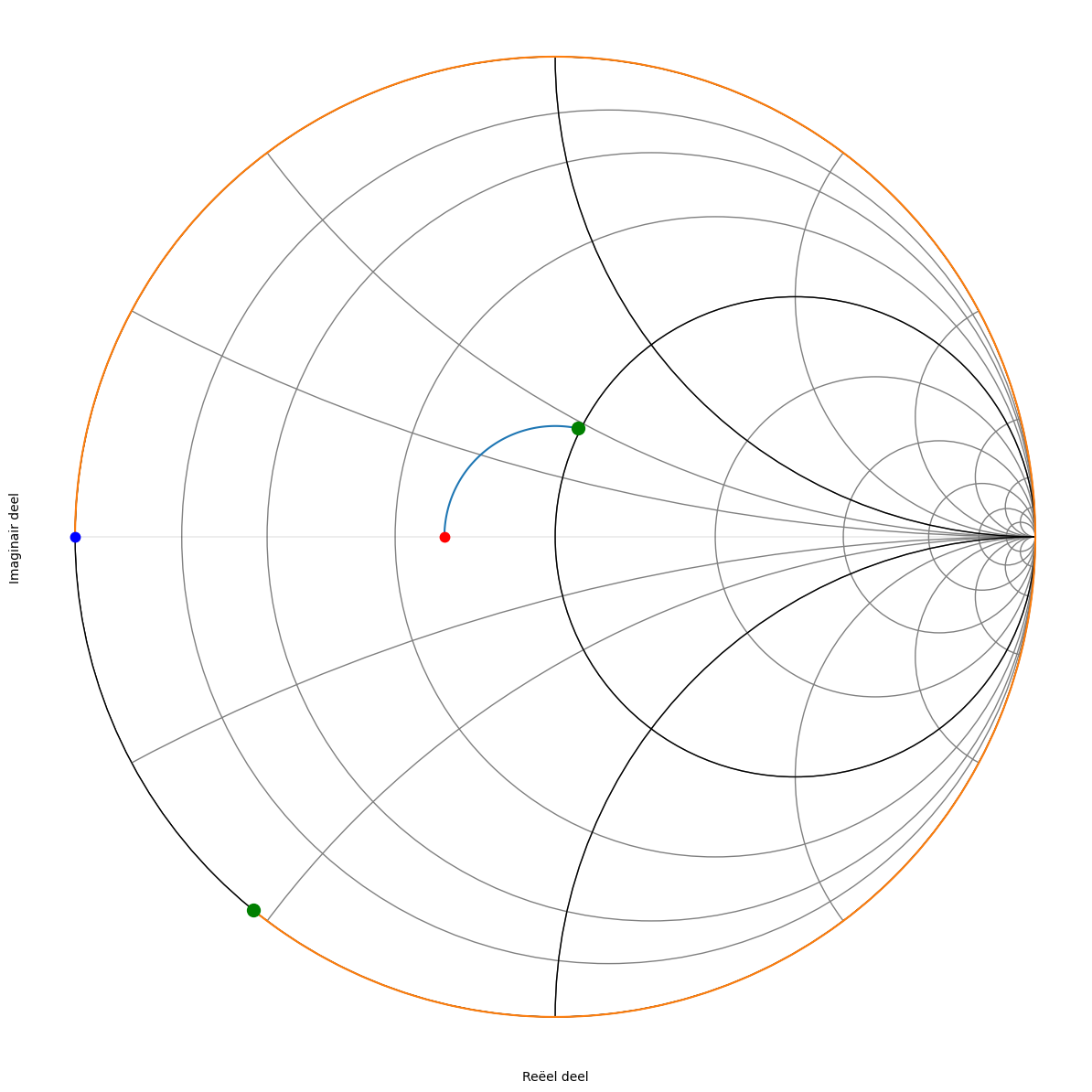
Fig. 153 Smith kaart van de zevende oplossing.

hoek    admitantie (Siemens)     lengte coax (cm)
 100    Y= 19.46+9.34j mS     lengte=6.94 cm
 101    Y= 19.62+9.39j mS     lengte=7.01 cm
 102    Y= 19.78+9.43j mS     lengte=7.08 cm
 103    Y= 19.94+9.47j mS     lengte=7.15 cm
 104    Y= 20.11+9.51j mS     lengte=7.22 cm

Overzicht van de bekomen admitantie als funktie van de hoek op de Smith kaart. De laatste kolom geeft de nodige lengte van de coax

hoek    admitantie (Siemens)     lengte coax (cm)
 305       Y= -10.41j mS     lengte=21.18 cm
 306       Y= -10.19j mS     lengte=21.25 cm
 307       Y= -9.97j mS     lengte=21.32 cm
 308       Y= -9.75j mS     lengte=21.39 cm
 309       Y= -9.54j mS     lengte=21.46 cm
 310       Y= -9.33j mS     lengte=21.53 cm

Overzicht van de bekomen admitantie als funktie van de hoek op de Smith kaart. De laatste kolom geeft de nodige lengte van de coax

Het stukje open coax dat we moeten voorzien ter vervanging van het spoel is dus: 21.46 cm

Het schema dat we nodig hebben om deze zevende oplossing te realiseren wordt dus:

Fig. 154 circuit van de zevende oplossing.

Oplossing 8: Oplossing 4 waarbij het spoel vervangen is door een kortgesloten transmissielijn

De y = 1 + j 0.47 compenseren we door -j 0.47 vertrekkende vanuit g=\(\infty\).

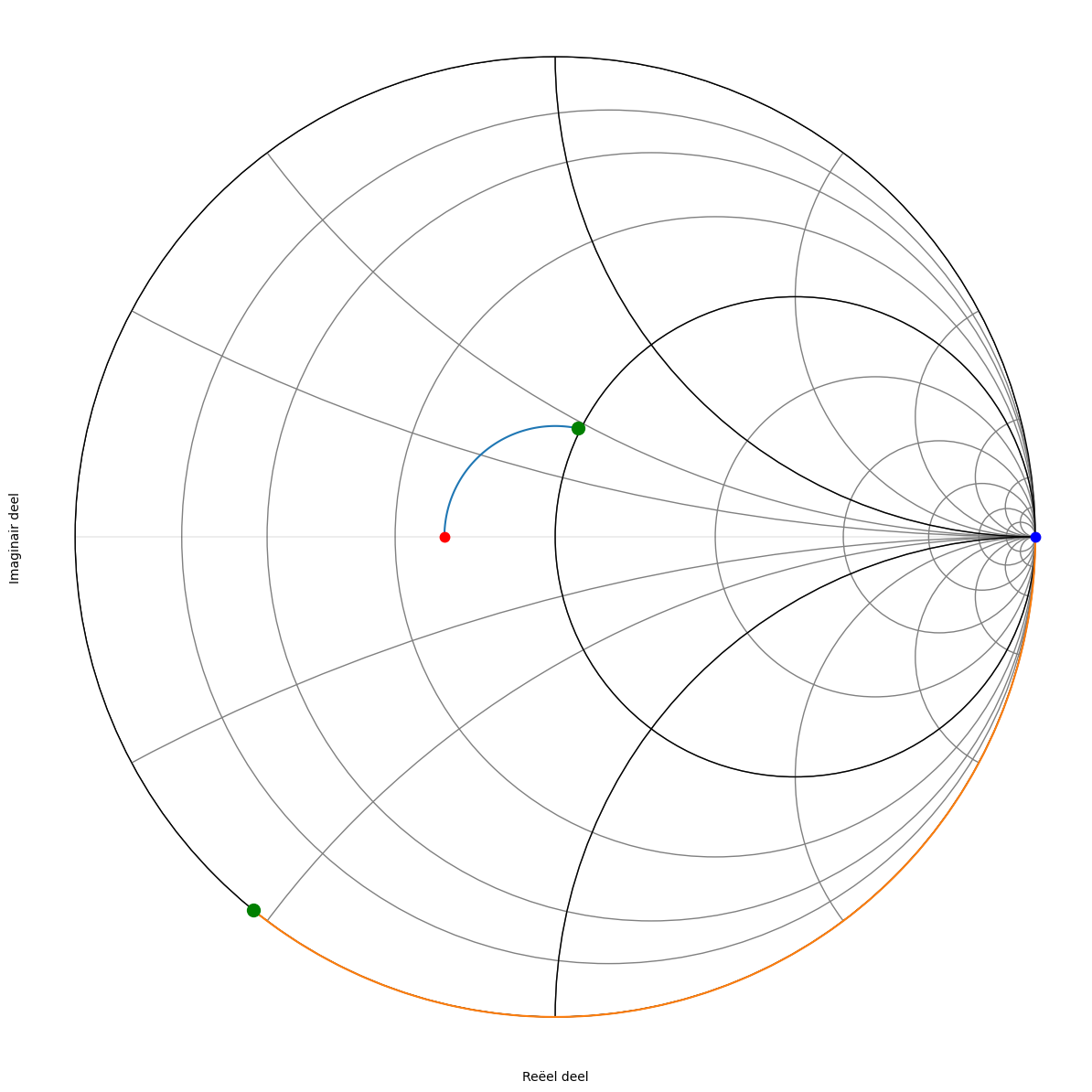
Fig. 155 Smith kaart van de achtste oplossing.

hoek    admitantie (Siemens)     lengte coax (cm)
 100    Y= 19.46+9.34j mS     lengte=6.94 cm
 101    Y= 19.62+9.39j mS     lengte=7.01 cm
 102    Y= 19.78+9.43j mS     lengte=7.08 cm
 103    Y= 19.94+9.47j mS     lengte=7.15 cm
 104    Y= 20.11+9.51j mS     lengte=7.22 cm
 105    Y= 20.28+9.55j mS     lengte=7.29 cm

Overzicht van de bekomen admitantie als funktie van de hoek op de Smith kaart. De laatste kolom geeft de nodige lengte van de coax

hoek    admitantie (Siemens)     lengte coax (cm)
 125       Y= -10.41j mS     lengte=8.68 cm
 126       Y= -10.19j mS     lengte=8.75 cm
 127       Y= -9.97j mS     lengte=8.82 cm
 128       Y= -9.75j mS     lengte=8.89 cm
 129       Y= -9.54j mS     lengte=8.96 cm
 130       Y= -9.33j mS     lengte=9.03 cm

Overzicht van de bekomen admitantie als funktie van de hoek op de Smith kaart. De laatste kolom geeft de nodige lengte van de coax

Het stukje kortgesloten coax dat we moeten voorzien ter vervanging van het spoel is dus: 9 cm

Het schema dat we nodig hebben om deze achtste oplossing te realiseren wordt dus:

Fig. 156 circuit van de achtste oplossing.