Reflecties#
Inleiding#
In dit hoofdstuk werken we een aantal voorbeelden uit die aangeven wat de invloed is van niet-aangepaste transmissielijnen op de signaalintegriteit. Om hierin inzicht te krijgen is de meest eenvoudige aanpak te kijken wat er gebeurt wanneer een ideale digitale puls wordt aangelegd aan de transmissielijn. In werkelijkheid moeten we natuurlijk beseffen dat de echte pulsvorm steeds eindige stijg- en daaltijd heeft (slew-rate) en dat bovendien de stroom die geleverd wordt door de output transistors ook niet constant is. Meer specifiek zal deze stroom afnemen wanneer de spanning over de transistor te klein wordt.
Een voorbeeld waarin een meer realistische pulsvorm in detail wordt uitgerekent tonen we hieronder. De video in Figuur 155 toont bovenaan een PCB met baantjes met een karakteristieke impedantie 50 Ohm. Onderaan vergelijken we de situatie waarbij er al dan niet een stukje met karakteristieke impedantie 32 Ohm in de transmissielijn wordt toegevoegd. In beide gevallen vertrekt aan de ingang een puls van 1 V. In het geval zonder een baantje met karakteristieke impedantie 32 Ohm meten we aan de uitgang na 80 ps een puls van 953 mV, dus terug bijna 1 V. De maximale reflectie, zoals we die kunnen meten aan de ingang, blijft kleiner dan 9 mV, verwaarloosbaar klein dus. In het geval met een baantje met karakteristieke impedantie 32 Ohm meten we aan de uitgang na 80 ps een puls van 813 mV. De maximale reflectie, zoals we die kunnen meten aan de ingang, is 314 mV.
Figuur 155 (boven) PCB waarbij de impedantie niet constant is (Rechts onder) groen: Bekomen signaal aan het einde van de getoonde transmissielijn. Rood: gereflecteerde signaal aan het begin. Het inkomende signaal is 1V#
De simulatie in Figuur 155 is numeriek uitgevoerd aan de hand van het simulatiepaket Ansys.
Voor het berekenen van reflecties kunnen twee gevallen onderscheiden, namelijk het geval dat karakteristieke impedantie \(Z_1\) gevolgd is door een transmissielijn met karakteristieke impedantie \(Z_2\) (zie Figuur 156) en het geval dat een transmissielijn met karakteristieke impedantie \(Z_1\) afgesloten is door een terminatieimpedantie \(Z_L\) (zie Figuur 157). We gaan beide gevallen op dezelfde manier gaan uitwerken aan de hand van een ladderdiagramma.
Figuur 156 Schematische voorstelling van een transmissielijn met karakteristieke impedantie \(Z_1\) gevolgd door een transmissielijn met impedantie \(Z_2\)#
Figuur 157 Schematische voorstelling van een transmissielijn met karakteristieke impedantie \(Z_1\) afgesloten met een terminatieimpedantie \(Z_L\)#
Uitwerken van een ladderdiagram#
Bij het uitwerken van een ladderdiagram volgen we hoe een ideale stap in aan de ingang loopt over de transmissielijn. Bij elke overgang waar de karakteristieke impedantie verandert, berekenen we de reflectie en de transmissie van het signaal. De reflectie \(\rho\) bij de overgang van de karakteristieke impedantie \(Z_1\) naar de karakteristieke impedantie \(Z_2\) bedraagt:
en de transmissie bedraagt \(1+\rho\)
Voor de gereflecteerde golf hebben we dan de vergelijkingen:
Voor de doorgaande golf hebben we dan de vergelijkingen:
Deze vergelijkingen voor de reflectie en de transmissie gelden zowel voor het geval dat de puls van transmissielijn 1 (met karakteristieke impedantie \(Z_1\)) overgaat naar een puls op transmissielijn 2 (met karakteristieke impedantie \(Z_2\)), zie Figuur 156, als voor het geval dat de puls van de transmissielijn afgesloten wordt door een belastingsimpedantie, zie Figuur 157.
Uitgewerkte voorbeelden#
We werken dit uit aan de hand van een aantal voorbeelden. Als eerste voorbeeld herbekijken we in tabelvorm het voorbeeld uit de video in Figuur 155. Er is geen reflectie aan de bron of aan het einde maar aan de overgang tussen de transmissielijk van 50 Ohm en de transmissielijn van 32 Ohm hebben we telkens een reflectie.
Figuur 158 Aangepaste transmissielijn met variatie in de dikte#
Tijdstip |
Spanning bron |
Puls in het eerste segment |
Spanning \(V_{1}\) |
Puls in het tweede segment |
Spanning \(V_{1}\) |
Puls in het derde segment |
Spanning einde |
|---|---|---|---|---|---|---|---|
\(T_{0}\) |
1 |
1 \(\rightarrow\) |
0 |
0 |
0 |
||
\(T_{1}\) |
1 |
-0.22 \(\leftarrow\) |
0.78 |
0.78 \(\rightarrow\) |
0 |
0 |
|
\(T_{2}\) |
0.78 |
0.78 |
0.172 \(\leftarrow\) |
0.952 |
0.952 \(\rightarrow\) |
0 |
|
\(T_{3}\) |
0.78 |
0.210 \(\leftarrow\) |
0.99 |
0.0378 \(\rightarrow\) |
0.952 |
0.952 |
|
\(T_{4}\) |
0.99 |
0.99 |
0.0083 \(\leftarrow\) |
0.9977 |
0.0461 \(\rightarrow\) |
0.952 |
|
\(T_{5}\) |
0.99 |
0.01 \(\leftarrow\) |
1.00 |
0.0018 \(\rightarrow\) |
0.9977 |
0.9977 |
|
\(T_{6}\) |
1.00 |
1.00 |
0.0004 \(\leftarrow\) |
0.9998 |
0.0022 \(\rightarrow\) |
0.9977 |
Het tweede voorbeeld Figuur 159 bestudeert een transmissielijn van 50\(\Omega\) die afgesloten is met een terminatieweerstand van 120\(\Omega\) en die een bronweerstand heeft in de driver chip van 30\(\Omega\).
Figuur 159 Transmissielijn met onaangepaste bronweerstand en terminatieweerstand.#
Het eerste dat we hierbij uitrekenen zijn de reflectiecoëfficiënten. We rekenen ook uit wat de initiële puls is die op de lijn vertrekt (\(V_{puls start}\)) en we kunnen uitrekenen wat de spanning op de lijn zal zijn na een oneindig aantal iteraties (\(V_{eind}\)).
Nu berekenen we het verloop van de puls over de lijn. Na elke reflectie wordt de puls kleiner (\(|\rho| < 1\)) en we tellen voor elk punt op de lijn de waarde van de spanning van de puls op telkens de puls is gepasseerd. Merk op dat aan het startpunt en aan het eindpunt er geen tijdsverschil is tussen de invallende en de gereflecteerde golf zodat we op deze punten beiden gelijktijdig moeten optellen. Het resultaat van deze simulatie zien we in Figuur 160
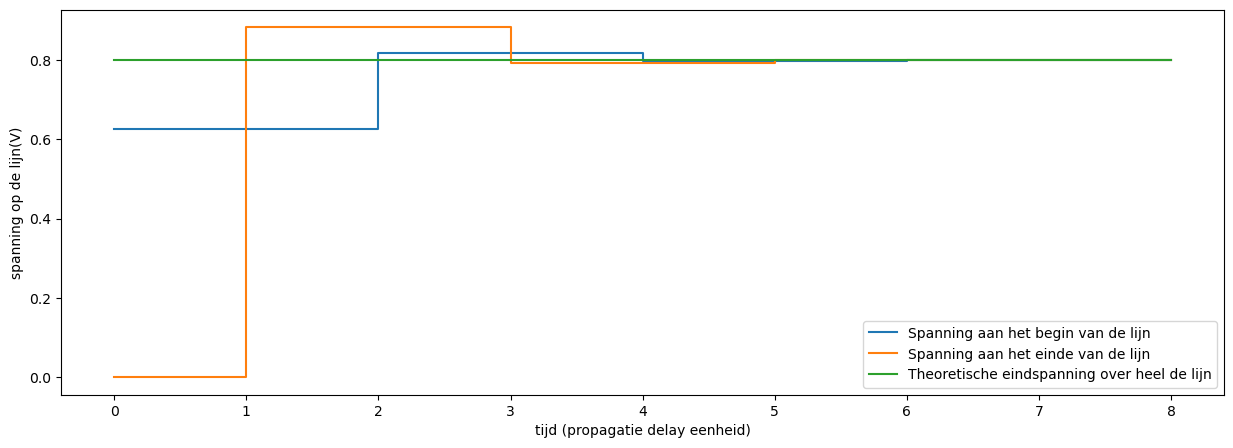
Figuur 160 Verloop van een 1V positieve puls op een 50 Ohm transmissielijn met een terminatieweerstand van 120 Ohm. De bronweerstand is 30 Ohm.#
We simuleren dit schema ook aan de hand van spice (zie Spice Listing 16) en dit aan de hand van 3 gevallen:
De stijgtijd van de bron (\(\tau_r\) = 0.1 ns) is veel korter dan de propagatietijd van de transmissielijn (\(\tau_d\) = 1 ns). Het resultaat zien we in Figuur 161.
De stijgtijd van de bron (\(\tau_r\) = 1 ns) is gelijk aan de propagatietijd van de transmissielijn (\(\tau_d\) = 1 ns). Het resultaat zien we in Figuur 162.
De stijgtijd van de bron (\(\tau_r\) = 6 ns) is veel langer dan de propagatietijd van de transmissielijn (\(\tau_d\) = 1 ns). Het resultaat zien we in Figuur 163.
.TITLE Transmission Line Example
Rs 1 2 30
O1 2 0 3 0 LOSSYMOD TD=2n
RL 3 0 120
.model LOSSYMOD ltra r=5.14 g=0 l=615E-9 c=246e-12 len=0.0812
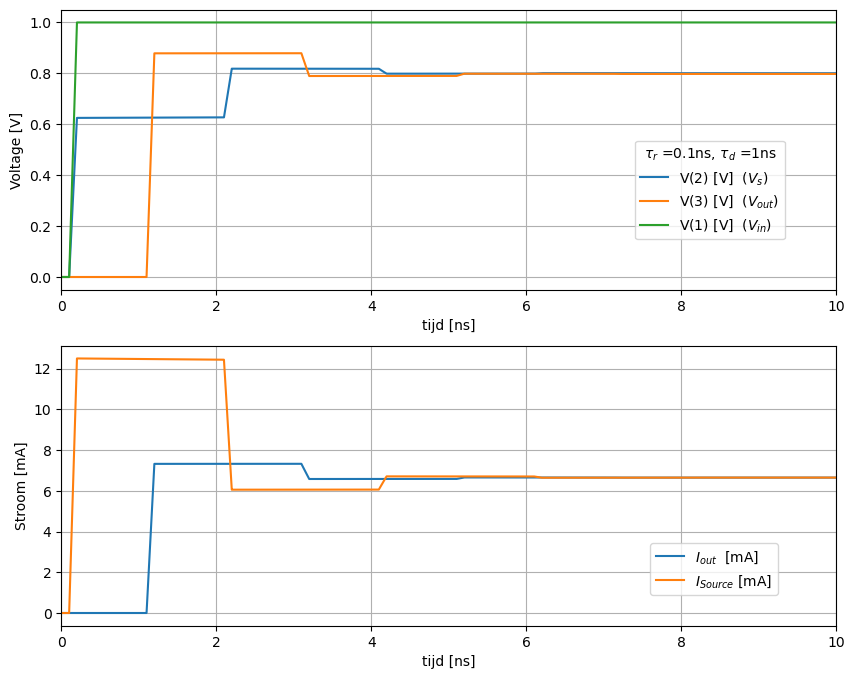
Figuur 161 Spice simulatie van een transmissielijn bij een stijgtijd 6 ns. De belasting is 120 Ohm load#
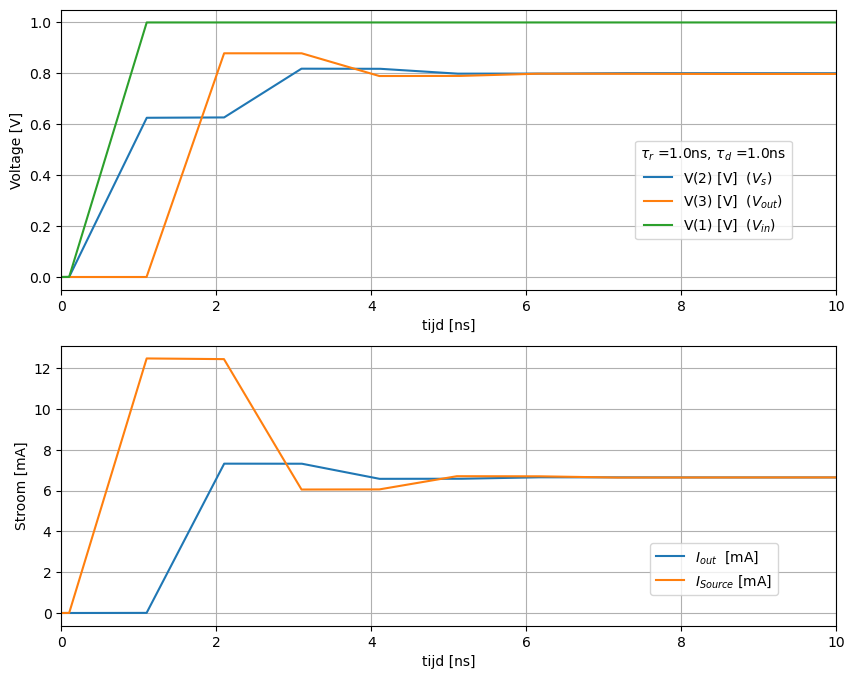
Figuur 162 Spice simulatie van een transmissielijn bij een stijgtijd 1 ns. De belasting is 120 Ohm load#
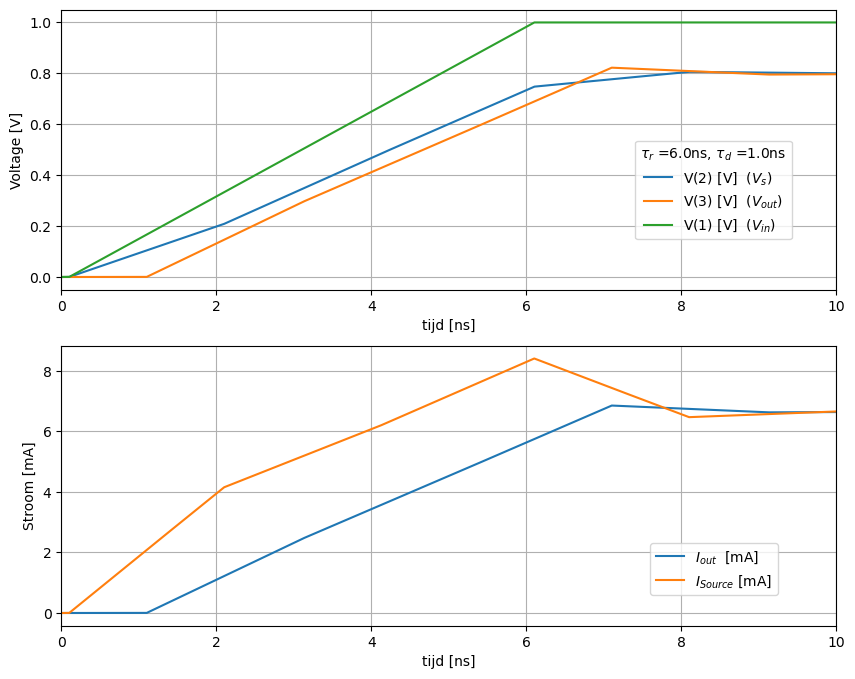
Figuur 163 Spice simulatie van een transmissielijn bij een stijgtijd 6 ns. De belasting is 120 Ohm load#
We simuleren dit schema ook aan de hand van spice (zie Spice Listing 17) en dit aan de hand van 3 gevallen:
De stijgtijd van de bron (\(\tau_r\) = 0.1 ns) is veel korter dan de propagatietijd van de transmissielijn (\(\tau_d\) = 1 ns). Het resultaat zien we in Figuur 164.
De stijgtijd van de bron (\(\tau_r\) = 1 ns) is gelijk aan de propagatietijd van de transmissielijn (\(\tau_d\) = 1 ns). Het resultaat zien we in Figuur 165.
De stijgtijd van de bron (\(\tau_r\) = 6 ns) is veel langer dan de propagatietijd van de transmissielijn (\(\tau_d\) = 1 ns). Het resultaat zien we in Figuur 166.
.TITLE Transmission Line with driver
MN1 0 1 2 0 NMOS w=150u L=0.50u
MP1 4 1 2 4 PMOS w=350u L=0.50U
VDD 4 0 1
O1 2 0 3 0 LOSSYMOD TD=2n
RL 3 0 120
.model LOSSYMOD ltra r=5.14 g=0 l=615E-9 c=246e-12 len=0.0812
.MODEL NMOS NMOS(LEVEL=1 VTO=0.05 KP=90.000E-6 LAMBDA=0.001)
.MODEL PMOS PMOS(LEVEL=1 VTO=-0.05 KP=55.000E-6 LAMBDA=0.001)
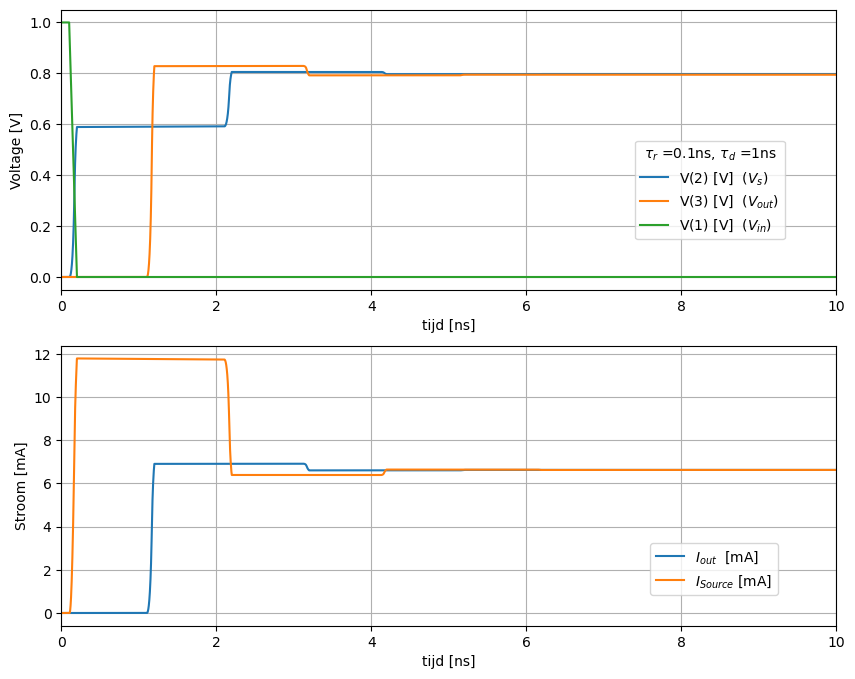
Figuur 164 Spice simulatie van een transmissielijn met driver bij een stijgtijd 100ps. De belasting is 120 Ohm load#
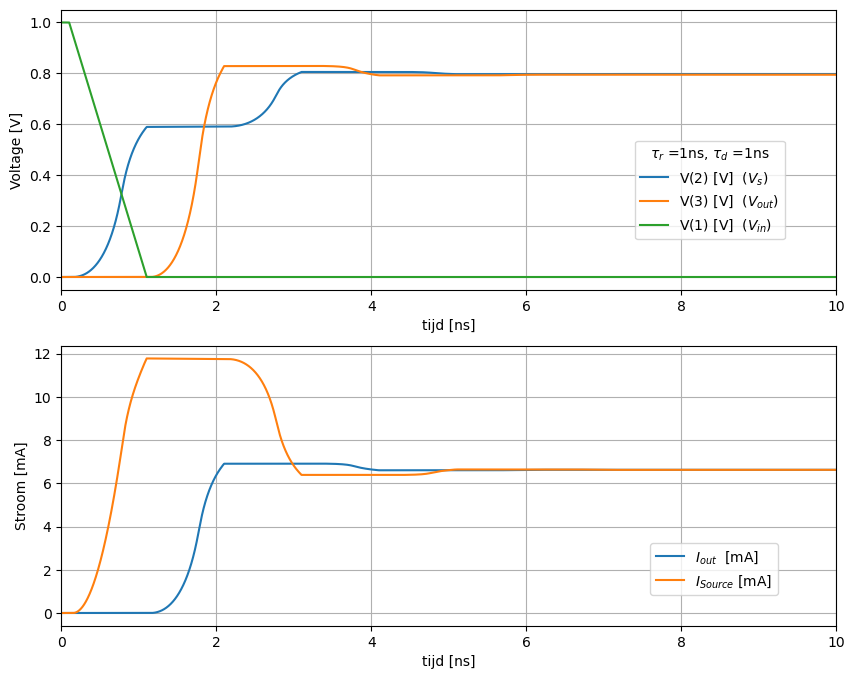
Figuur 165 Spice simulatie van een transmissielijn met driver bij een stijgtijd 1 ns. De belasting is 120 Ohm load#
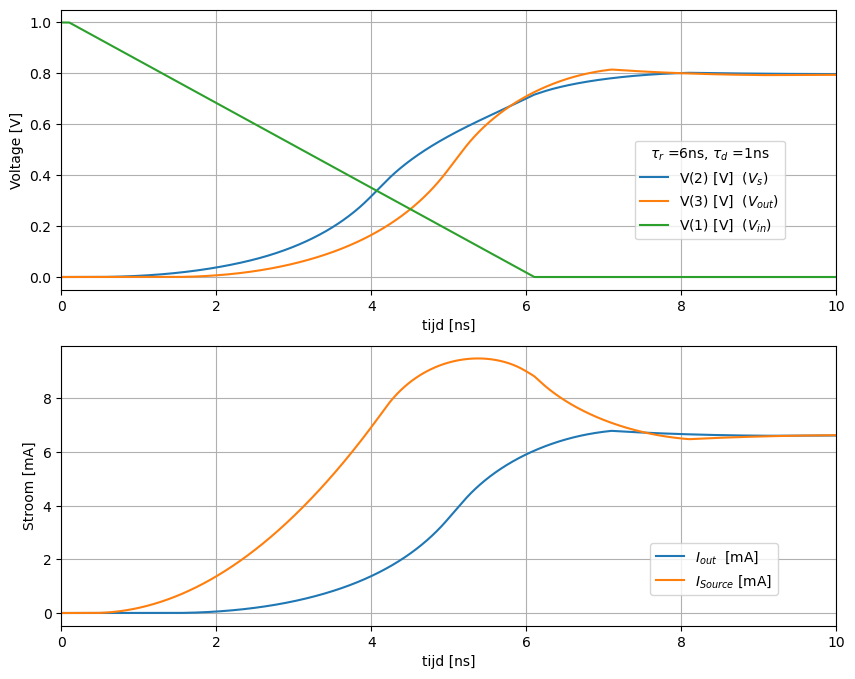
Figuur 166 Spice simulatie van een transmissielijn met driver bij een stijgtijd 6 ns. De belasting is 120 Ohm load#
We kunnen het theoretisch ladderdiagramma ook uitwerken voor een praktische propagatievertraging van 1.5ns en een pulse gestuurd door een IC van met een voedingsspanning op de uitgangsbuffers van 3.3 V. De aan-weerstand van de uitgangsbuffers is 10 Ohm (de aanweerstand van de pMOS) en de terminatieweerstand van de lijn is 25 Ohm (zie ladder2schem). In dat geval verloopt de stijgende puls theoretisch zoals in Figuur 167
Ook hier rekenen we de reflectiecoëfficiënten uit.
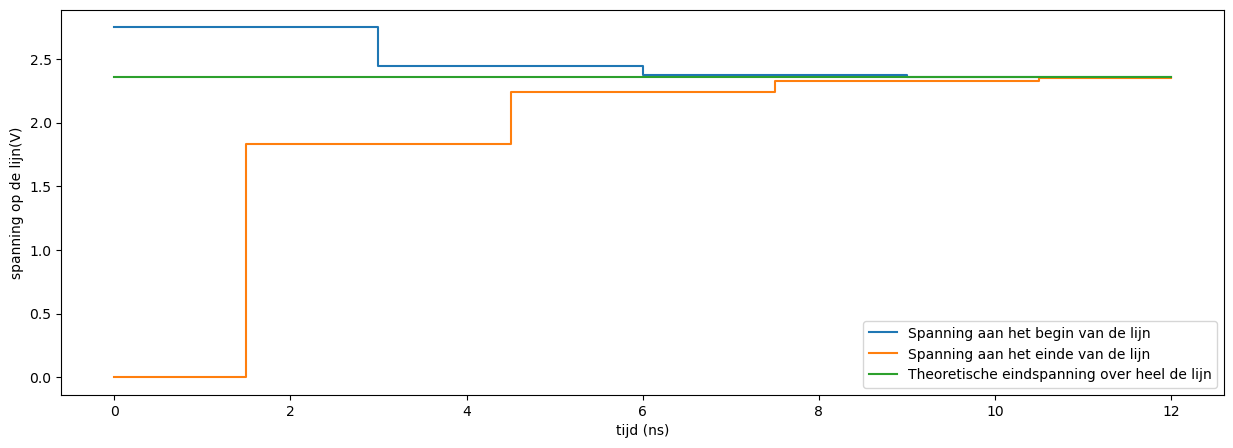
Figuur 167 Verloop van een 3.3V positieve puls op een 50 Ohm transmissielijn met een terminatieweerstand van 25 Ohm. De bronweerstand is 10 Ohm.#
We simuleren dit schema ook aan de hand van spice (zie Spice Listing 18) en dit aan de hand van 3 gevallen:
De stijgtijd van de bron (\(\tau_r\) = 0.1 ns) is veel korter dan de propagatietijd van de transmissielijn (\(\tau_d\) = 1.5 ns). Het resultaat zien we in Figuur 168.
De stijgtijd van de bron (\(\tau_r\) = 1 ns) is gelijk aan de propagatietijd van de transmissielijn (\(\tau_d\) = 1.5 ns). Het resultaat zien we in Figuur 169.
De stijgtijd van de bron (\(\tau_r\) = 9 ns) is veel langer dan de propagatietijd van de transmissielijn (\(\tau_d\) = 1.5 ns). Het resultaat zien we in Figuur 170.
.TITLE Transmission Line Example
Rs 1 2 10
O1 2 0 3 0 LOSSYMOD TD=2n
RL 3 0 25
.model LOSSYMOD ltra r=5.14 g=0 l=615E-9 c=246e-12 len=0.1219
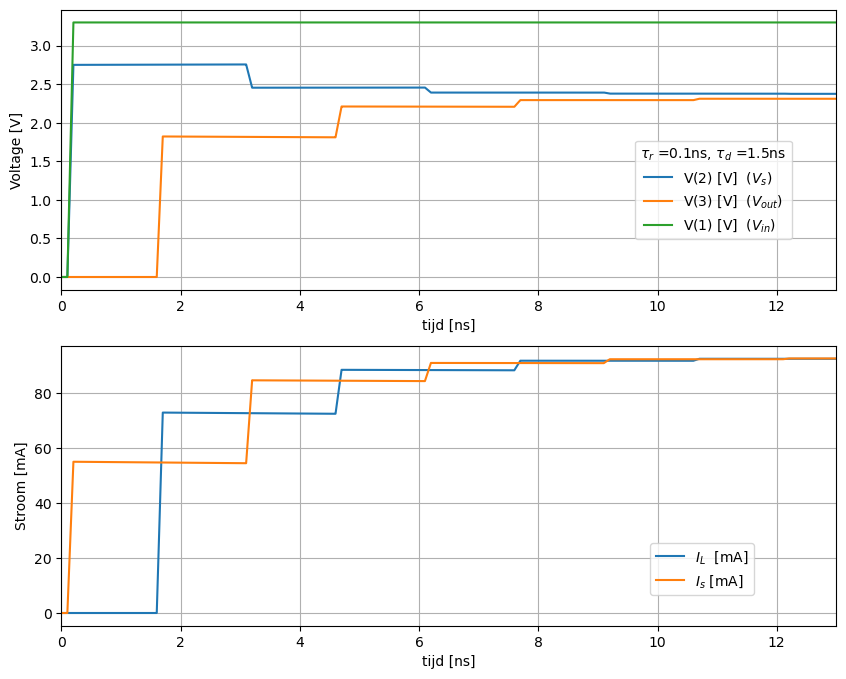
Figuur 168 Spice simulatie van een transmissielijn bij een stijgtijd 01ns. De belasting is 25 Ohm load#
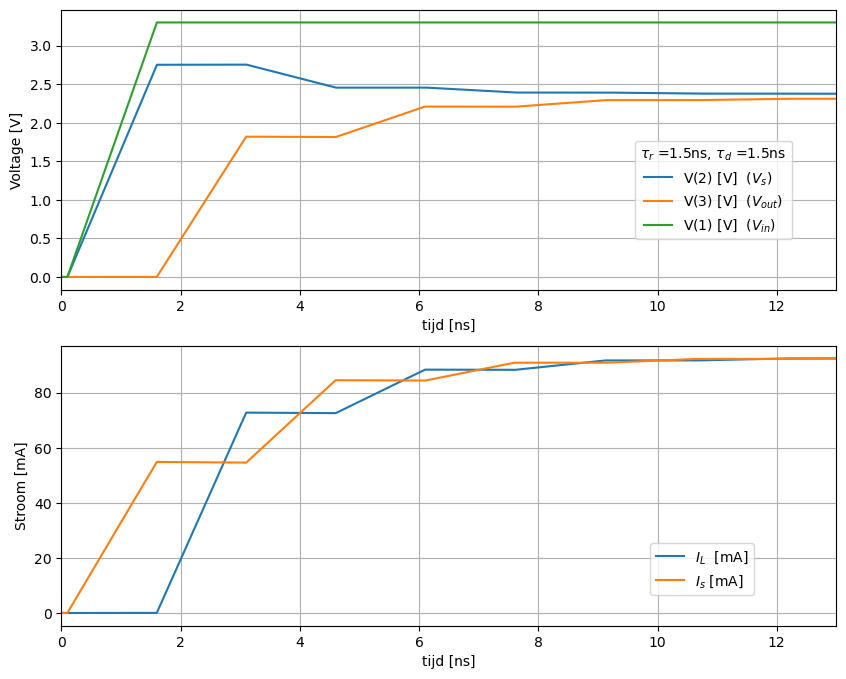
Figuur 169 Spice simulatie van een transmissielijn bij een stijgtijd 1.5ns. De belasting is 25 Ohm load#
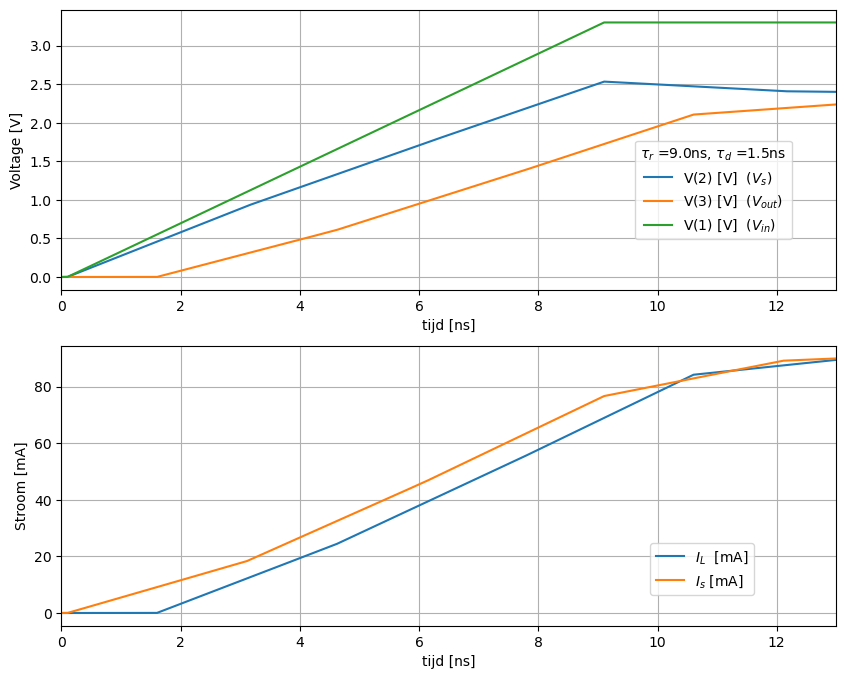
Figuur 170 Spice simulatie van een transmissielijn bij een stijgtijd 9ns. De belasting is 25 Ohm load#
We simuleren dit schema ook aan de hand van spice (zie Spice Listing 19) en dit aan de hand van 3 gevallen:
De stijgtijd van de bron (\(\tau_r\) = 0.1 ns) is veel korter dan de propagatietijd van de transmissielijn (\(\tau_d\) = 1.5 ns). Het resultaat zien we in Figuur 171.
De stijgtijd van de bron (\(\tau_r\) = 1 ns) is gelijk aan de propagatietijd van de transmissielijn (\(\tau_d\) = 1.5 ns). Het resultaat zien we in Figuur 172.
De stijgtijd van de bron (\(\tau_r\) = 9 ns) is veel langer dan de propagatietijd van de transmissielijn (\(\tau_d\) = 1.5 ns). Het resultaat zien we in Figuur 173.
.TITLE Transmission Line with driver
MN1 0 1 2 0 NMOS w=150u L=0.50u
MP1 4 1 2 4 PMOS w=350u L=0.50U
VDD 4 0 3.3
O1 2 0 3 0 LOSSYMOD TD=2n
RL 3 0 25
.model LOSSYMOD ltra r=5.14 g=0 l=615E-9 c=246e-12 len=0.1219
.MODEL NMOS NMOS(LEVEL=1 VTO=0.50 KP=90.000E-6 LAMBDA=0.001)
.MODEL PMOS PMOS(LEVEL=1 VTO=-0.45 KP=55.000E-6 LAMBDA=0.001)
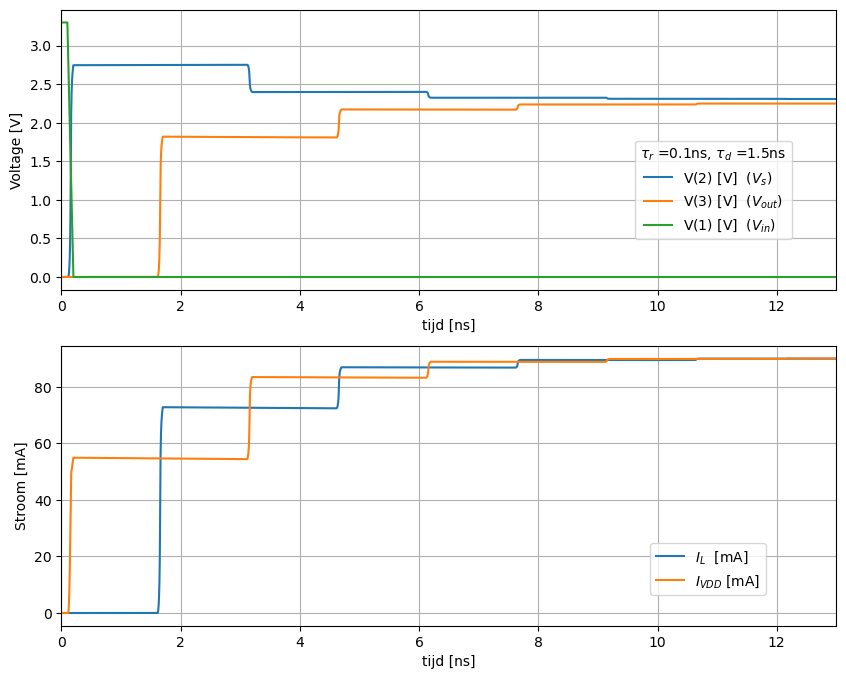
Figuur 171 Spice simulatie van een transmissielijn met driver bij een stijgtijd 100ps. De belasting is 25 Ohm load#
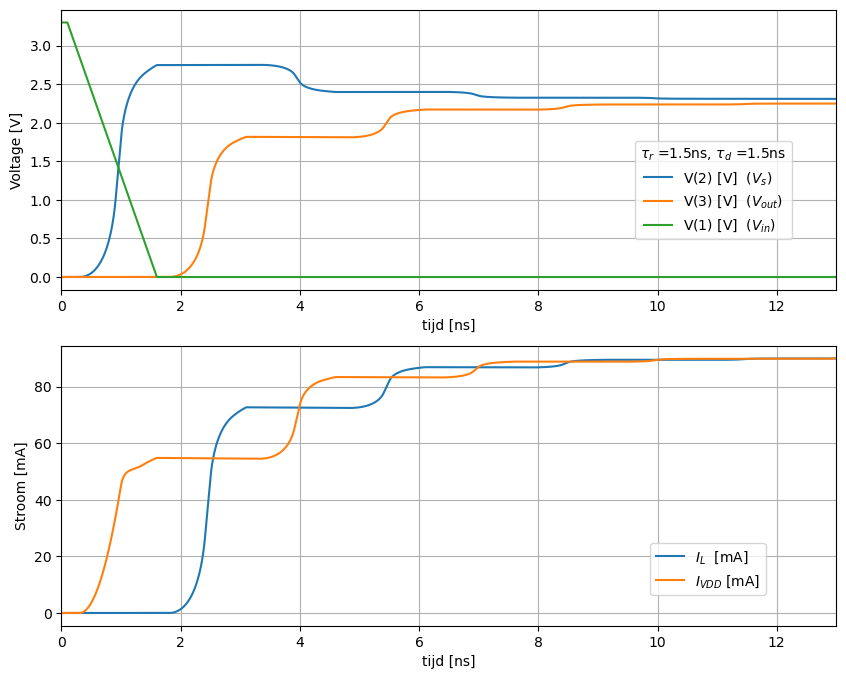
Figuur 172 Spice simulatie van een transmissielijn met driver bij een stijgtijd 1.5ns. De belasting is 25 Ohm load#
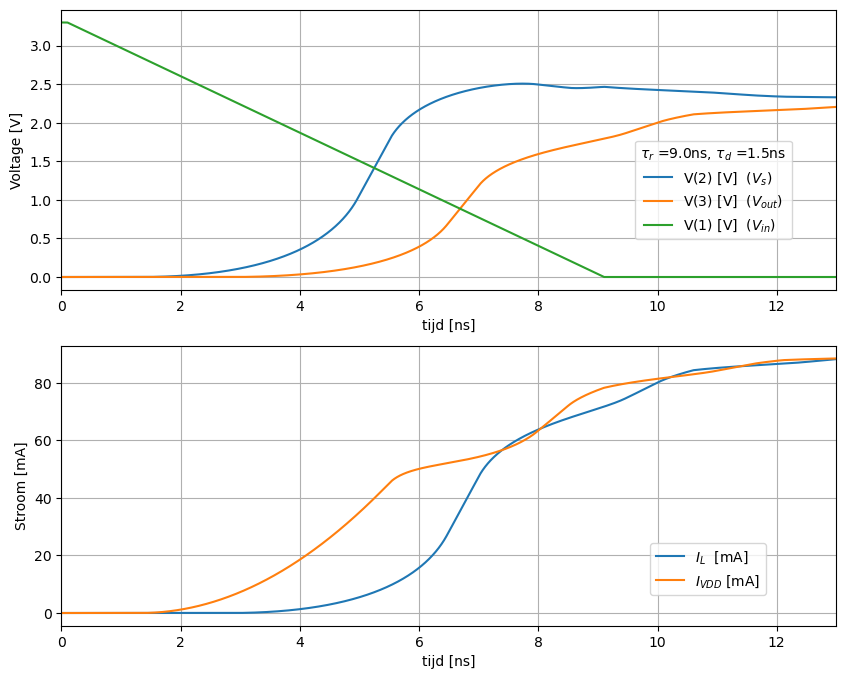
Figuur 173 Spice simulatie van een transmissielijn met driver bij een stijgtijd 9ns. De belasting is 25 Ohm load#