Klasse C Versterkers

In de vorige hoofdstukken hebben we de laagfrequent versterkers besproken. Dit zijn versterkers met typisch een relatief grote bandbreedte. Verder hebben we de laagfrequent versterkers verder opgedeeld in de versterkers met 1 vermogen transistor in de vermogentrap (Klasse A) en de versterkers met 2 of meer vermogentransistors in de vermogentrap (Klasse B en Klasse G). In dit hoofdstuk bestuderen we de klasse C versterker. Beide versterkers zijn resonante versterkers die bestaat uit een LRC trilkring (of meerdere LC kringen) die aangestuurd wordt door een enkele transistor. Als een gevolg hiervan werkt deze versterker op een vaste frequentie of binnen een zeer beperkte bandbreedte rond deze centrale frequentie. Deze bandbreedte is typisch maximaal 1\(\%\) van de resonantie frequentie. In Tabel 1 geven we een overzicht van deze verschillende versterkers.

Tabel 1 Indeling van de vermogenversterkers

	laagfrequent of breedband	hoogfrequent of resonant
1 transistor in de vermogentrap	Klasse A	Klasse C Klasse F Klasse E
2 of meer transistors in de vermogentrap	Klasse B Klasse G	Klasse D

De toepassingen liggen in de eerste plaats in het domain van de telecomunicatie waar de Klasse C versterker gebruikt wordt om signalen door te sturen, gemoduleerd op de draaggolf van de zender. Deze draaggolf heeft typisch een vaste frequentie. Daarnaast zijn er nog industriele toepassingen mogelijk, zoals bijvoorbeeld het inductief verwarmen (zoals in smeltovens) of het dielectrisch verwarmen (voor het drogen, bakken en polymeriseren).

basisprincipe van de werking

Het basisprincipe is steeds als het volgt: We gebruiken de eigenfrequentie van een resonante kring om de oscillatie op de juiste frequentie te genereren en om harmonischen weg te filteren. Deze resonante kring vormt de belasting van de vermogentransistor. De vermogentransistor levert het vermogen dat verloren/uitgestraald wordt door de resonante kring.

Fig. 6 toont het basisschema van de klasse C versterker.

Fig. 6 Basisschema van de Klasse C versterker.

We maken gebruik van de eigenfrequentie van de resonante kring om de oscillatie op de juiste frequentie te genereren en om de harmonischen weg te filteren. De resonante kring verliest vermogen tijdens de trilling en de vermogentransistor zal dit vermogen terug toevoegen aan de kring. Dit gebeurt door korte stroompulsen te leveren.

Differentiaalvergelijking van de trilkring

Voordat we de werking van de versterker bekijken, bestuderen we in meer detail de trilkring en de bekomen trilling die we bekomen indien de trilling spontaan verloopt (i.e. niet aangestuurd door de transistor). Het schema dat we hiervoor bestuderen kan je zien in Fig. 7

Fig. 7 Trilkring van de Klasse C versterker.

Om de werking van dit schema te berekenen schrijven we de eerste wet van Kirkhoff op in de gemeenschappelijke knoop en de stroom-spanningsvergelijkingen op voor elk element. Deze vergelijkingen zijn:

\[ I_C+ I_R + I_L =0 \]

\[ Q_C= C V \]

\[ I_R R_L = V \]

\[ L \frac{d I_L}{dt} = V \]

De stroom naar de condensator (\(I_C\)) kunnen we door de lading van de condensator (\(Q_C\)) af te leiden naar de tijd, dus \(I_C =\frac{d Q_C}{dt}\). Hierdoor hebben we alle vergelijkingen reeds als functie van de stroom, namelijk:

\[ I_C+ I_R + I_L =0 \]

\[ I_C= C \frac{d V}{dt} \]

\[ I_R R_L = V \]

\[ L \frac{d I_L}{dt} = V \]

Aangezien de stroom-spanningsvergelijking van het spoel de afgeleide van de stroom bevat, kunnen we de eerste wet van Kirkhoff niet onmiddellijk gebruiken, maar we kunnen wel de afgeleide van deze wet gebruiken. De vergelijkingen worden dan:

\[ \frac{d I_C}{dt}+ \frac{d I_R}{dt} + \frac{d I_L}{dt} =0 \]

\[ \frac{d I_C}{dt}= C \frac{d^2 V}{dt^2} \]

\[ \frac{d I_R}{dt} =\frac{1}{R_L} \frac{d V}{dt} \]

\[ \frac{d I_L}{dt} =\frac{1}{L} V \]

Invullen geeft dan:

\[C \frac{d^2 V}{dt^2} + \frac{1}{R_L} \frac{d V}{dt} + \frac{1}{L} V = 0\]

Deze vergelijking kunnen we oplossen door de Laplace transformatie te nemen van de functie \(V(t)\). De bekomen oplossing is dan:

\[V(t)= V_o \cos(\omega t +\phi) \exp(-\beta t)\]

\[ \beta=\frac{1}{2 R_L C} \]

\[ \omega =\sqrt{\frac{1}{L C}- \beta^2}\]

Waarbij \(V_o\) en \(\phi\) de integratieconstanten zijn. Fig. 8 toont deze oplossing voor een uitdempende trilling van 50 V rond een spanning van 80 V. In het rood is de spanning aangegeven die we elke periode verliezen en die dus moet gecompenseerd worden om de trilling op gang te houden.

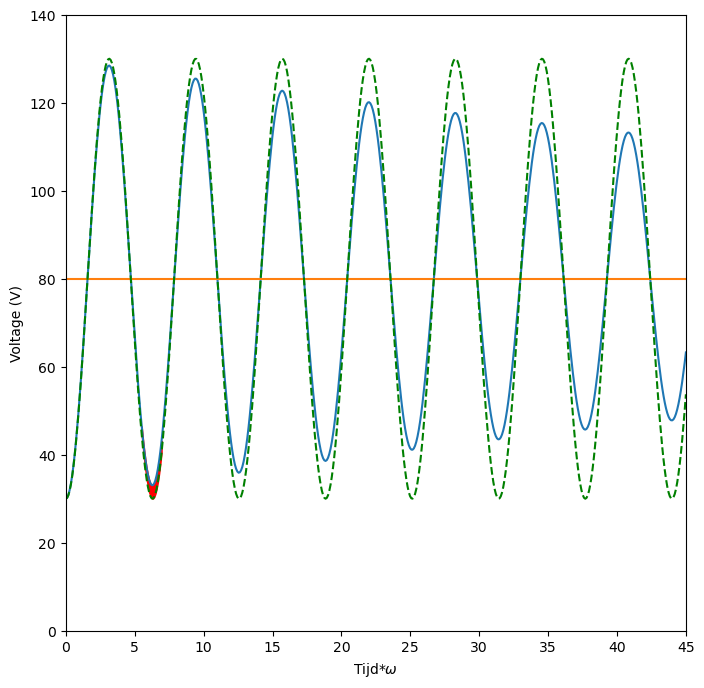
Fig. 8 Voorbeeld van een gedempte trilling van 50V rond een referentiespaning van 80V

Keuze van de parameters van de resonante kring

Om een vermogenversterker te ontwerpen die actief is bij een bepaalde frequentie moeten in eerste instantie de parameters van de resonante kring gekozen worden, namelijk \(L_1\) en \(C_1\). Deze parameters kunnen we bepalen op basis van de gegevens die de ingenieur normaal in een ontwerp opgave ter beschikking krijgt, namelijk de impedantie van de belasting \(R_L\) en het maximum vermogen \(P_{AC}\) dat moet geleverd kunnen worden op de frequentie \(\omega\). Het is belangrijk dat we \(\beta <<< \omega\) kiezen. In eerste instantie kunnen we bijvoorbeeld vertrekken van \(\beta = 0.1 \omega\), waarna we dan

\[ \beta=\frac{1}{2 R_L C_1} \]

gebruiken om de condensator \(C_1\) te kiezen. Vervolgens gebruiken we

\[ \omega =\sqrt{\frac{1}{L_1 C_1}- \beta^2}\]

om de waarde van de spoel \(L_1\) te kiezen.

Merk op:

Aangezien we in de meeste gevallen \(\beta <<< \omega\) kiezen kunnen we in deze gevallen vaak de resonatiefrequentie benaderen als:

\[ \omega =\sqrt{\frac{1}{L_1 C_1}}\]

Vervolgens gebruiken we de formule

\[ P_{AC} =\frac{V_{AC}^2}{2 R_L}\]

om de spanningsamplitude te \(V_{AC}\) te berekenen en dus daaruit ook de nodige voedingsspanning \(V_{DD}\).

Opdracht 2 (Ontwerpparameters klasse C versterker)

Ontwerp een Klasse C versterker die gebruik maakt van een λ/2 antenne die een stralingsimpedantie heeft van 60 Ohm, om 10 W AC-vermogen uit te zenden op 104.7 MHz. Kies geschikte waardes voor de capaciteit C1 en de inductantie L1. Bepaal ook de nodige voedingsspanning VDD

Aansturingsprincipe van de versterker

Het basis werkingsprincipe van de Klasse C versterker is als het volgt: We leggen een sinusvormige spanning met een negatieve offset aan de hand van een serieweerstand aan aan de basis van de bipolaire transistor. De ingang van de bipolaire transistor vormt een diode naar de emitter en als gevolg hiervan loopt er enkel een basisstroom wanneer de ingangspanning positief is. Deze basisstroom wordt dan een factor \(\beta_F\) versterkt in de collectorstroom. Deze gepulste collectorstroom wordt dan aangelegd aan de LRC trilkring.

De originele beschrijving van dit aansturingsprincipe kan je vinden in [1].

Fig. 9 Basisschema van de Klasse C versterker met een eenvoudig schema om de versterker aan te sturen.

De onderstaande Widget laat toe te kijken wat de impact is van de instellingen aan de basis op de bekomen collector stroom. We leggen aan \(V_{in}\) een negatieve DC spanning aan en een iets grotere AC spanningsamplitude. Dit heeft tot gevolg dat de spanning aan \(V_{in}\) slechts een beperkt deel van de periode boven de 0.6V komt, wat de spanning is die nodig is om de basis-emitter junctie van de bipolaire transistor in geleiding te brengen. De hoeveelheid stroom die we krijgn wordt bepaald door \(R_{in}\) en deze stroom wordt dan vervolgens versterkt met een factor \(\beta_F\) wat dan de collectorstroom oplevert.

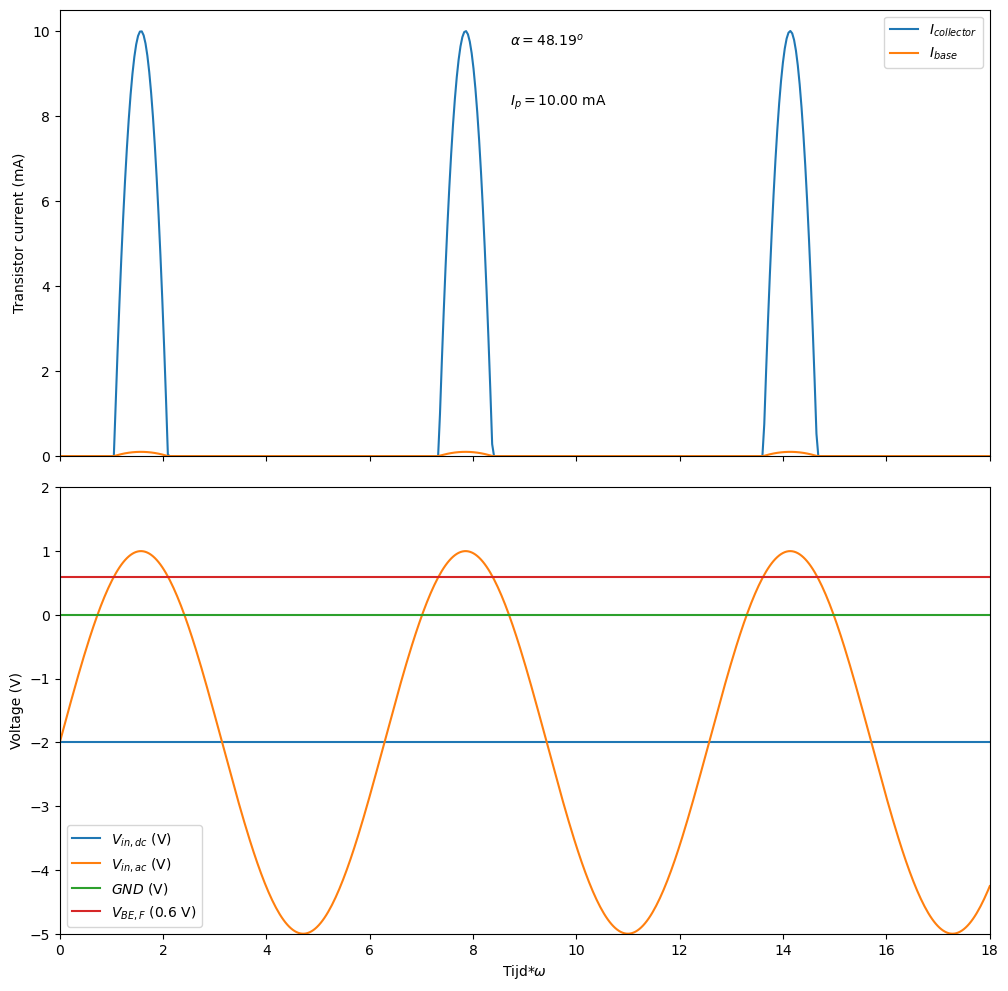
Fig. 10 Instelling van de basisstroom om de gepaste geleidingshoek en piekstroom te krijgen.

De LRC kring is een parallel LRC kring. Een parallel LRC kring heeft de eigenschap dat hij een aangelegde gepulste stroomsignaal gaat omzetten in een sinusvormige spanning op de resonantiefrequentie. Aangezien de spanning over de belasting (\(R_L\)) dan sinusvormig is, gaat de stroom door de belasting ook sinusvormig zijn.

De overeenkomende SPICE code voor dit circuit is:

Spice Listing 5 basis Klasse C circuit

* Class C amp 1
Q_Q1         2 1 0 Q2
L_L1         2 3  1uH
C_C1         2 3  10nF
R_RL         2 3  60
V_Vdd        3 0 11V
R_Rin        4 1 100
V_Vin        4 0 sin(-1.5 2.7 1591500) DC=-1.5
.model Q2  NPN(Is=14.34f BF=200)

In de .model kaart zien we dat we voor de bipolaire transistor een model gebruiken dat we Q2 hebben genoemd. Dit zijn biploaire transistors waar we een \(\beta_{Forward}\) hebben gelijk aan 200.

Het circuit waarbij we de knoopnummers een rood label gegeven hebben wordt dan:

Fig. 11 Basisschema waarbij we de knopen genummerd hebben overeenkomende met de spice code.

Een spice simulatie van het bovenstaande circuit levert hetvolgende op:

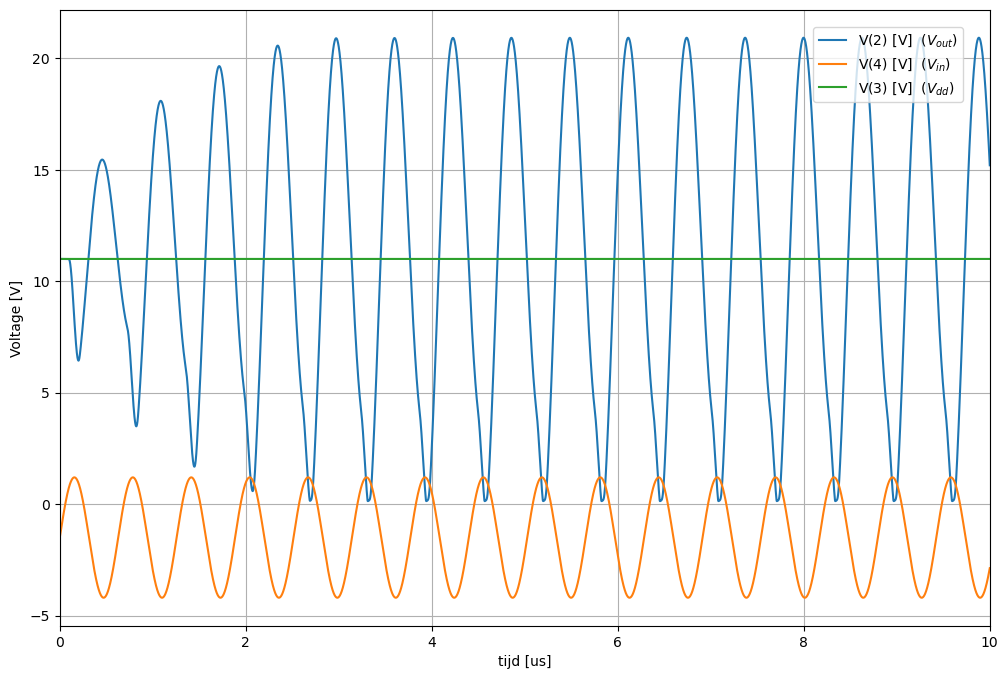
Fig. 12 Spanningen bekomen na een spice simulatie van de klasse C versterker.

We merken op dat het ongeveer een 5-tal periodes duurt eer de een AC zwaai bekomen wordt die gelijk is aan de voedingsspanning (i.e. 11V). Dit aantal periodes is sterk afhankelijk van de gekozen trilkring.

We kunnen ook de collectorstroom plotten na dezelfde simulatie.

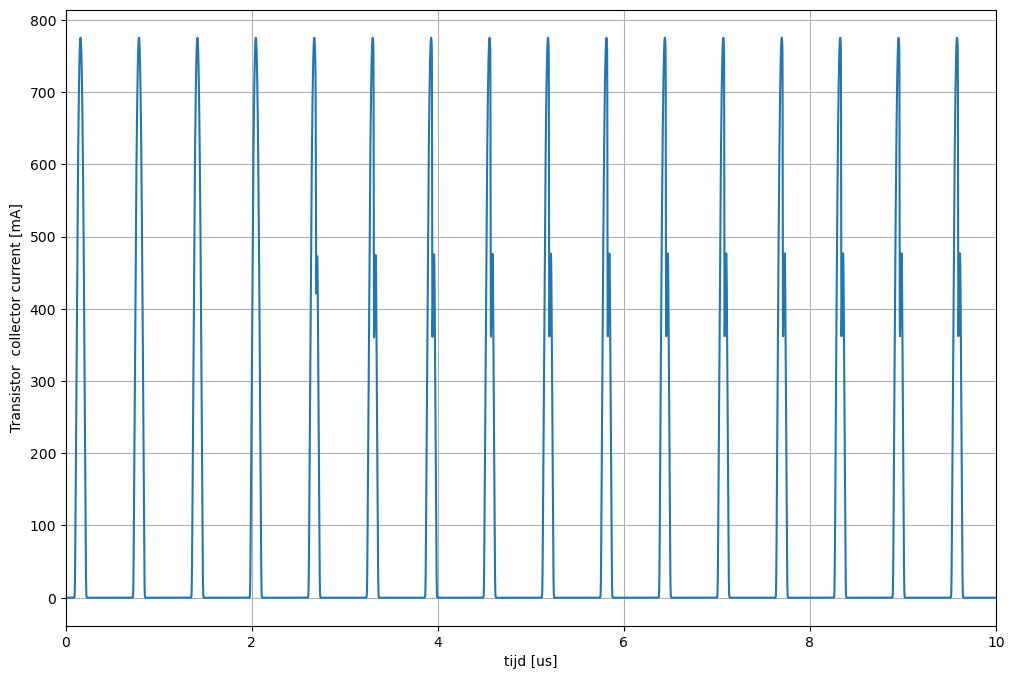
Fig. 13 Stromen bekomen na een spice simulatie van de klasse C versterker.

Dit circuit werd ontworpen voor een collector piekstroom van 600 mA. We merken op dat de collectorstromen bij het starten van de oscillatie eventjes boven de ontwerplimiet komen. Wanneer dit een probleem vormt moet de geleidingshoek groter gemaakt worden. We merken ook op dat de stroom terug daalt wanneer de bipolaire transistor in verzadiging geraakt. Dit is ook logisch. Als de spanning tussen de collector en de emitter te klein wordt, kan er geen stroom meer lopen.

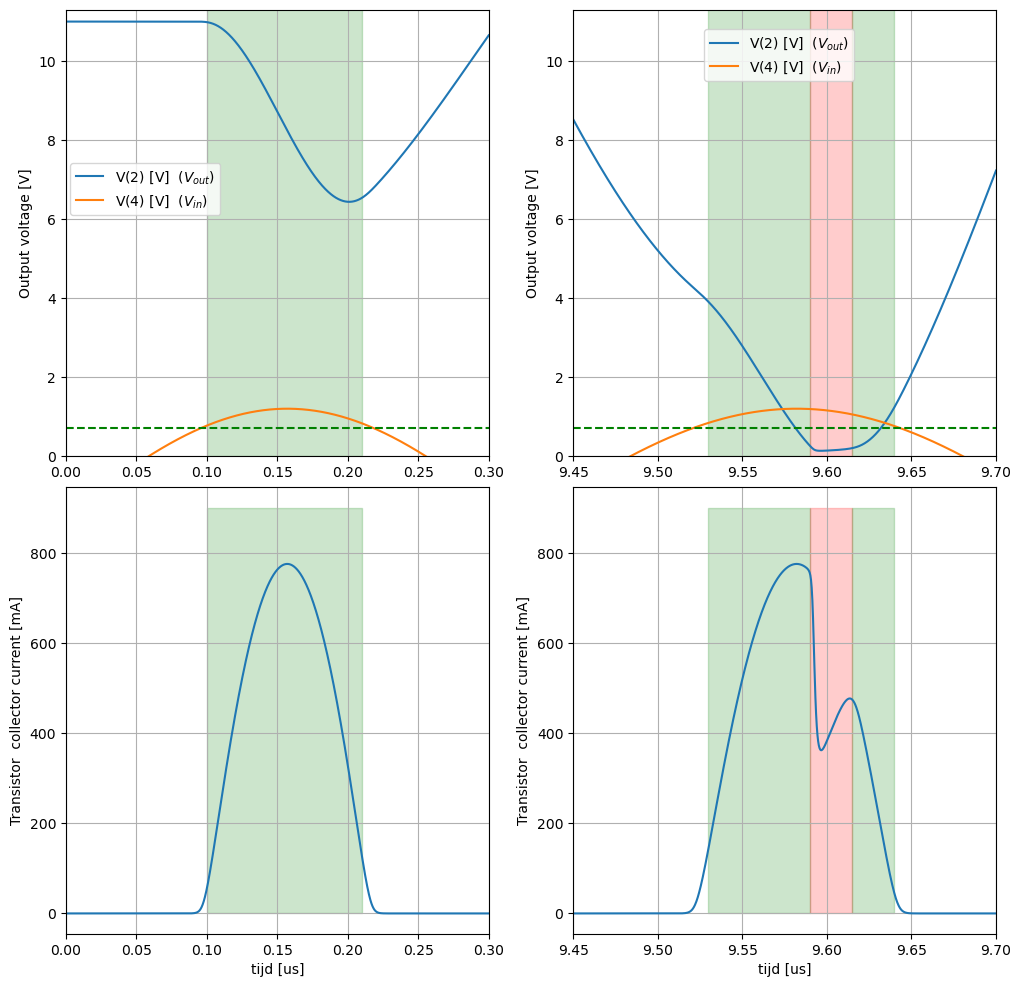
Fig. 14 Detail van de spanningen en stromen (spice simulatie) van de klasse C versterker: (links) opstart van de oscillatie (rechts) stuurperiode waarbij de bipolaire transistor gedurende een deel van de stuurperiode in verzadiging komt (in het rood aangegeven).

We kunnen ook een Lissajous figuur plotten van de uitgangsspanning ten opzichte van de ingangsspanning. We merken dat er een toenemend faseverschil is dat tijdens de periode dat de transistor in geleiding is terug weggewerkt wordt.

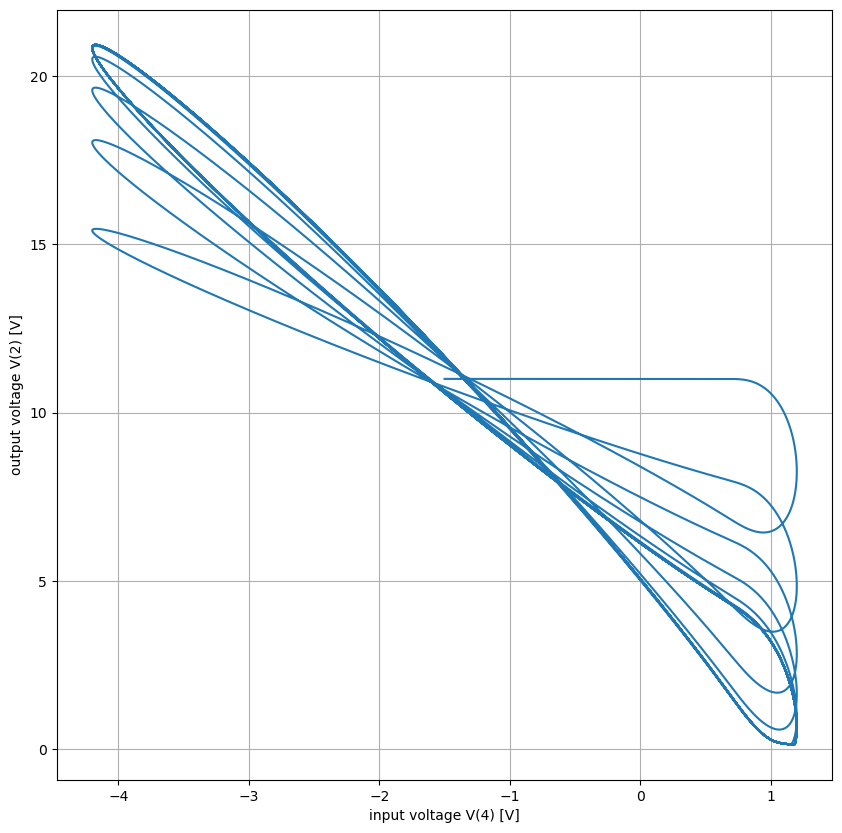
Fig. 15 Lissajous figuur van de spanning op knoop 2 als functie van de spanning op knoop 4.

Wanneer we kijken naar het basis circuit van de klasse C versterker hebben we 2 elementen die voornamelijk bijdragen tot het bepalen van de oscillatiefrequentie, namelijk:

• \(L_1\)

• \(C_1\)

en 4 elementen die bijdragen to het optimaliseren van et bekomen vermogen, namelijk:

• De belastingsweerstand \(R_L\)

• De voedingsspanning \(V_{dd}\)

• De piekstroom van de transistor \(I_p\)

• Het gedeelte van de periode dat de transistor aangestuurd wordt : 2\(\alpha\)

In wat volgt zullen we eerst exploreren welke van de 4 bovenstaande parameters het bekomen vermogen bepalen. Vervolgens zullen we een methodologie uitwerken om de optimale parameters te selecteren. In het volgende deel gaan we dan verder met de selectie van \(L_1\) en \(C_1\)

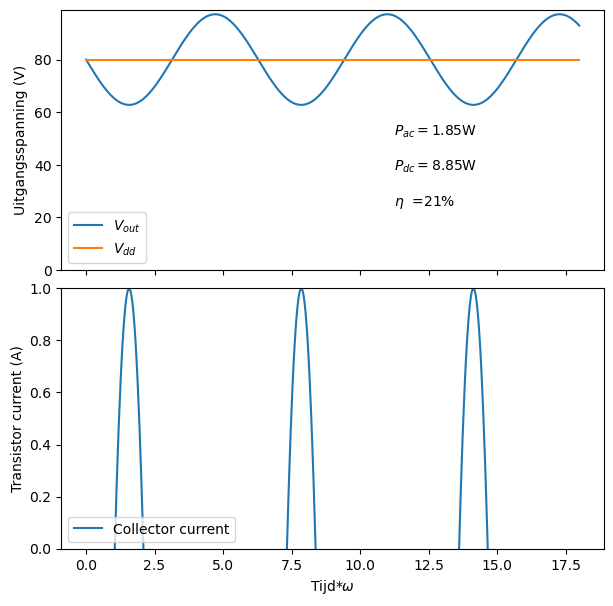
Fig. 16 Bekomen oscillatie bij de gekozen ontwerpparameters.

In de bovenstaande grafiek is de uitgangspanning \(V_{out}\)

(1)\[V_{out}(t)=V_{dd}-V_a \cos(\omega t) \]

en is de collector current van de transistor \(I_c\)

(2)\[ I_c(t) = \left\{ \begin{matrix} \frac{\cos(\omega t)-\cos(\alpha)}{1-\cos(\alpha)}I_p & wanneer & |\omega t| <\alpha \ 0 & wanneer& | \omega t| >\alpha \end{matrix} \right.\]

Hoe we aan de waarde van \(V_a\) komen, volgt in de afleiding hieronder.

Op basis van de hierboven gegeven stromen en spanningen kunnen we de verschillende vermogens uitrekenen (met \(u=\omega t\)):

(3)\[ P_{ac} = \frac{1}{2\pi}\int_{-\pi}^{\pi}{\frac {(V_a\sin(u))^2}{R_L} du } = \frac {V_a^2}{2 R_L} \]

(4)\[ P_{dc} = \frac{1}{2\pi}\int_{-\alpha}^{\alpha} { V_{dd}I_c(u) du } = \frac{V_{dd} I_p}{\pi}\frac {\sin(\alpha)-\alpha\cos(\alpha)}{1-\cos(\alpha)} \]

(5)\[ P_{T} = \frac{1}{2\pi}\int_{-\alpha}^{\alpha} { V_{out}(u)I_c(u) du } = \frac{V_{dd} I_p}{\pi}\frac {\sin(\alpha)-\alpha\cos(\alpha)}{1-\cos(\alpha)}- \frac {I_p V_a}{4 \pi}\frac{(2\alpha-\sin(2\alpha))}{(1-\cos(\alpha))} \]

Nu is het totale DC vermogen (\(P_{dc}\))de som van het in de transistor gedisipeerde vermogen (\(P_{T}\)) en het bekomen nuttige vermogen (\(P_{ac}\)):

(6)\[ P_{ac} = P_{dc}-P_{T} \]

Op basis van vergelijkingen (3),(4) en (5) bekomen we:

(7)\[ \frac {V_a^2}{2 R_L} =\frac{I_p V_a}{4 \pi} \frac {(2\alpha-\sin(2\alpha))}{(1-\cos(\alpha))}\]

De bekomen amplitude van oscillatie is:

(8)\[ V_a= \frac{I_p R_L}{2 \pi} \frac{ 2 \alpha - \sin(2 \alpha)}{1-\cos(\alpha)} \]

Het is goed om voor al deze 4 parameters ook eens de instantane bekomen power en het instantane ingangsvermogen te bekijken.

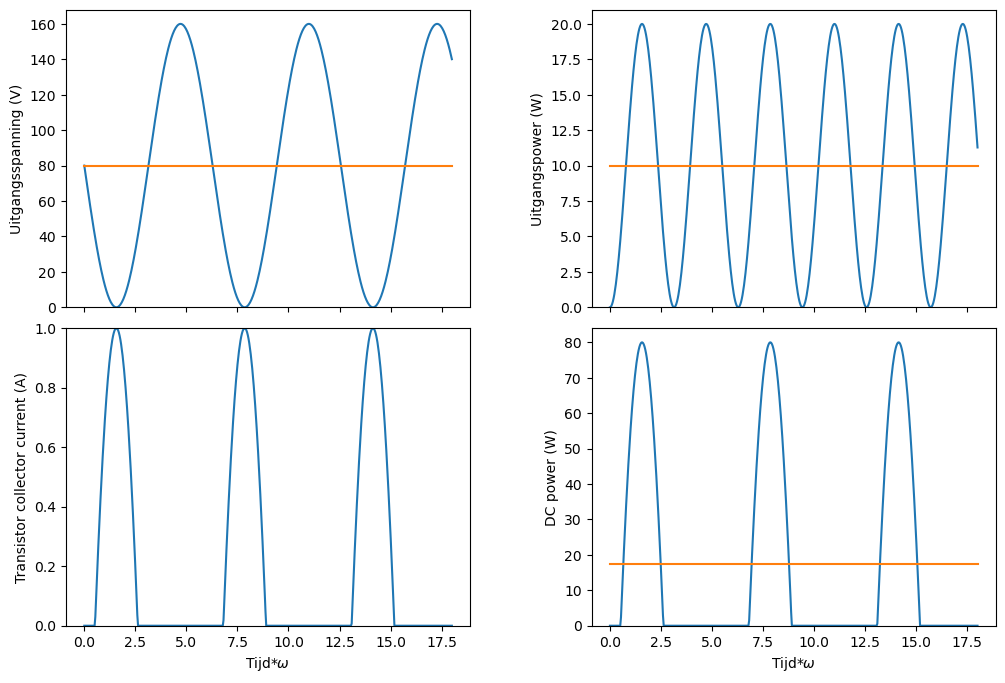
Fig. 17 Uitgangspower en DC power als functie van de tijd en de verschillende signalen.

Vervolgens kijken we naar het instantane vermogenverlies in de transistor:

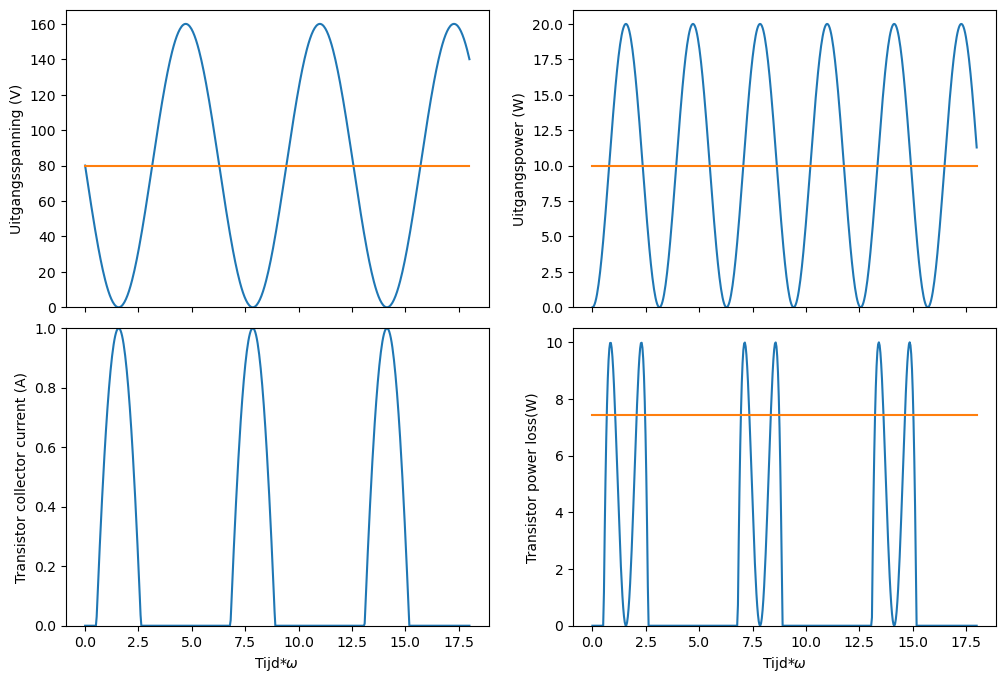
Fig. 18 Transistor power verlies als functie van de tijd en de verschillende signalen.

Voor het bepalen van het verlies in de transistor plotten we bij voorkeur de relatie tussen de spanning over de transistor en de stroom door de transistor.

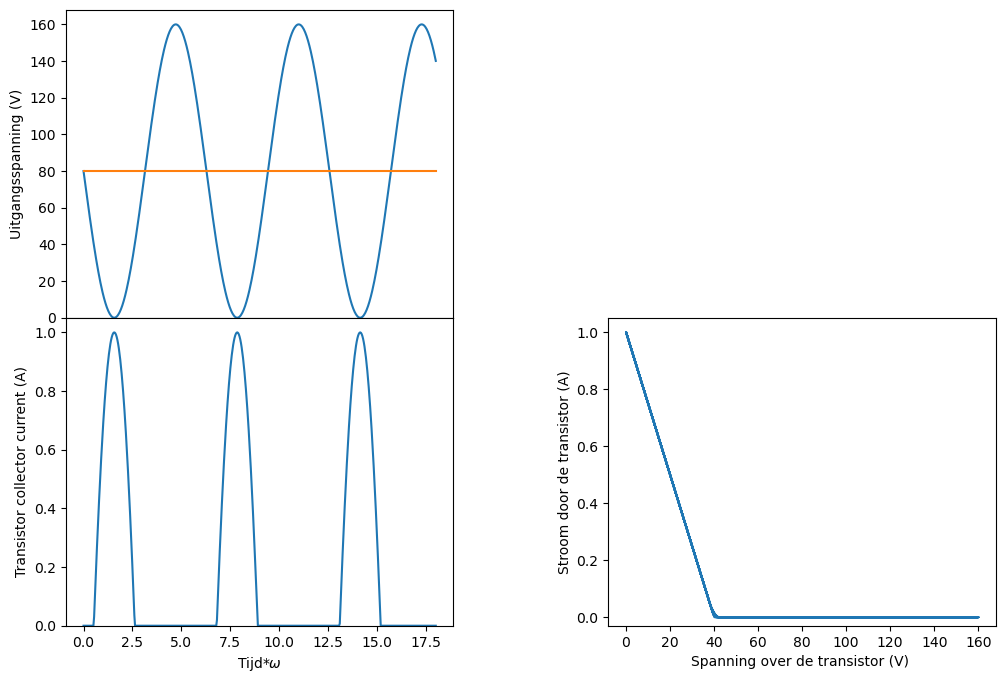
Fig. 19 De stroom door de transistor als functie van spanning over de transistor bij de verschillende instellingen.

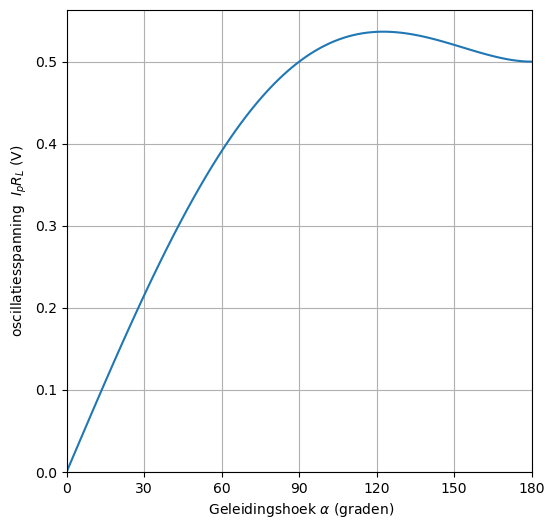
Fig. 20 bekomen oscillatiespanning als functie van de geleidingshoek.

opmerking:

• De grafiek in deze jupyter notebook geeft de maximale oscillatiespanning \(V_{max}\) weer die bekomen wordt in de resonante kring in functie van de geleidingshoek (\(\alpha\)) ten opzichte van het product van de piekstroom \(I_p\) en de weerstand \(R_L\). Dus de plot geeft dus de waarde van \(u= \frac{V_{max}}{I_p R_L}\)

• De grafiek in de powerpoint slides van de les geeft het maximale vermogen \(P_{max}\) dat bekomen wordt in functie van de geleidingshoek ten opzichte van het product van de piekstroom Ip en de voedingspanning. \(P_{max} =\frac{V_{max} I_{max}}{2}\). Dus de plot is \(w=\frac{P_{max}}{V_{DD} I_p} = \frac{\frac{V_{max}*I_{max}}{2}}{V_{DD} I_p} = \frac{V_{max} \frac{Vmax}{2 R_L}}{Vdd I_p}\). Bovendien weten we dat \(V_{max}< V_{DD}\) en in het beste geval (= verzadiging) \(V_{max}\) gelijk wordt aan \(V_{DD}\). Dus bij verzadiging geldt \(w=\frac{Vmax}{2 R_L I_p}\)

In de meeste gevallen willen we \(V_{DD}\) als oscillatie amplitude. Daarom zullen we \(I_p\) kiezen als:

\[ I_{p,max}= 2 \pi \frac{V_{DD} }{R_L} \frac{1-\cos(\alpha)}{ 2 \alpha - \sin(2 \alpha)}\]

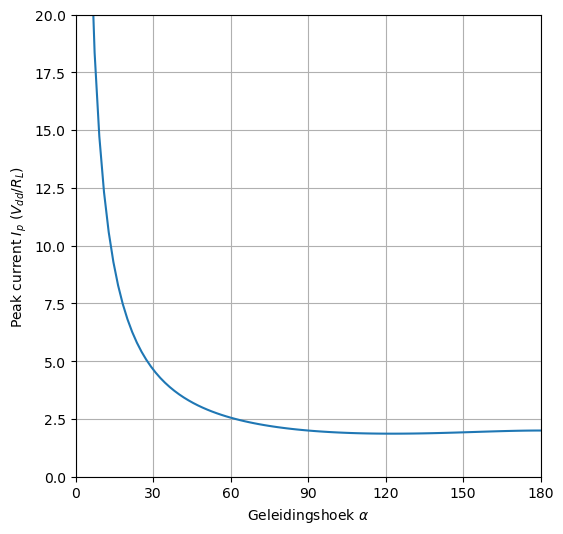
Fig. 21 De nodige piekstroom om een amplitude te bekomen die gelijk is aan de voedingsspanning als een functie van de geleidingshoek.

\[P_{ac}=I_p^2 R_L \frac{(2 \alpha-\sin (2 \alpha))^2}{8 \pi ^2 (1-\cos (\alpha))^2}\]

\[P_{dc}=\frac{V_{dd} I_p}{\pi}\frac {\sin(\alpha)-\alpha\cos(\alpha)}{1-\cos(\alpha)}\]

Het rendement wordt dan, rekening houdende met dat \(I_p\) niet groter mag worden dan \(I_{P,max}\)

\[ \eta=\frac{I_p R_L}{V_{dd}}\frac{(2 \alpha-\sin (2 \alpha))^2}{8 \pi (1-\cos (\alpha)) (\sin (\alpha)-\alpha \cos (\alpha))} \]

Maximale uitsturing

Omdat we het maximale rendement gaan bekomen bij maximale uitsturing kunnen we voor \(I_p\) de bekomen waarde van \(I_{p,max}\) invullen:

\[ \eta=\frac{2 \alpha-\sin (2 \alpha)}{4 (\sin (\alpha)-a \cos (\alpha))} \]

En als bekomen vermogen bekomen we:

\[ P_{ac,max}(\alpha)= \frac{V_{dd}^2 }{2 R_L} \]

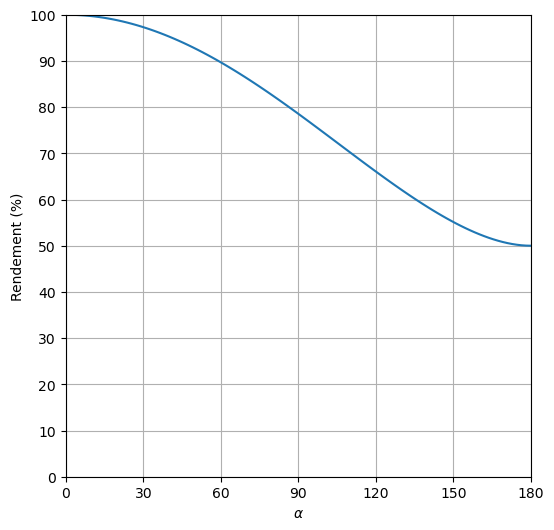
Fig. 22 Bekomen rendement bij maximale uitsturing.

Opdracht 3 (Keuze van de geleidingshoek)

Een belasting met een weerstand van 60 Ohm wensen we te gebruiken om 1 W over te brengen op 1.591 MHz, aan de hand van een vermogentransistor met een maximale stroom van 660 mA Kies geschikte waardes voor de capaciteit C1, de inductantie L1, de voedingsspanning VDD en de hoek α. Hoe groot is het rendement? Wat kiezen we als de maximale stroom van de transistor 360 mA is?

De LRC kring als functie van de frequentie

De klasse C versterker legt stroompulsen aan over een RLC parallel-kring. Als gevolg hiervan worden sinusvormige spanningen bekomen. Hiervoor splitsen we de aangelegde stroompulsen op in al zijn frequentiecomponenten en voor elke component bepalen we dan de overeenkomende spanning aan de hand van de impedantie \(Z(\omega)\): \( V(\omega)=Z(\omega)* I(\omega)\). De formule voor \(Z(\omega)\) is:

\[ Z(\omega)=\frac{1}{j \omega C+\frac{1}{R_L}+\frac{1}{j \omega L}} \]

De onderstaande figuur toont \(Z(\omega)\) als functie van de frequentie. L en C bepalen de frequentie. Er is een kleine invloed van \(R_L\) op de frequentie. De invloed van \(R_L\) op de bandbreedte en op hoe snel de trilling uitdempt is echter veel groter.

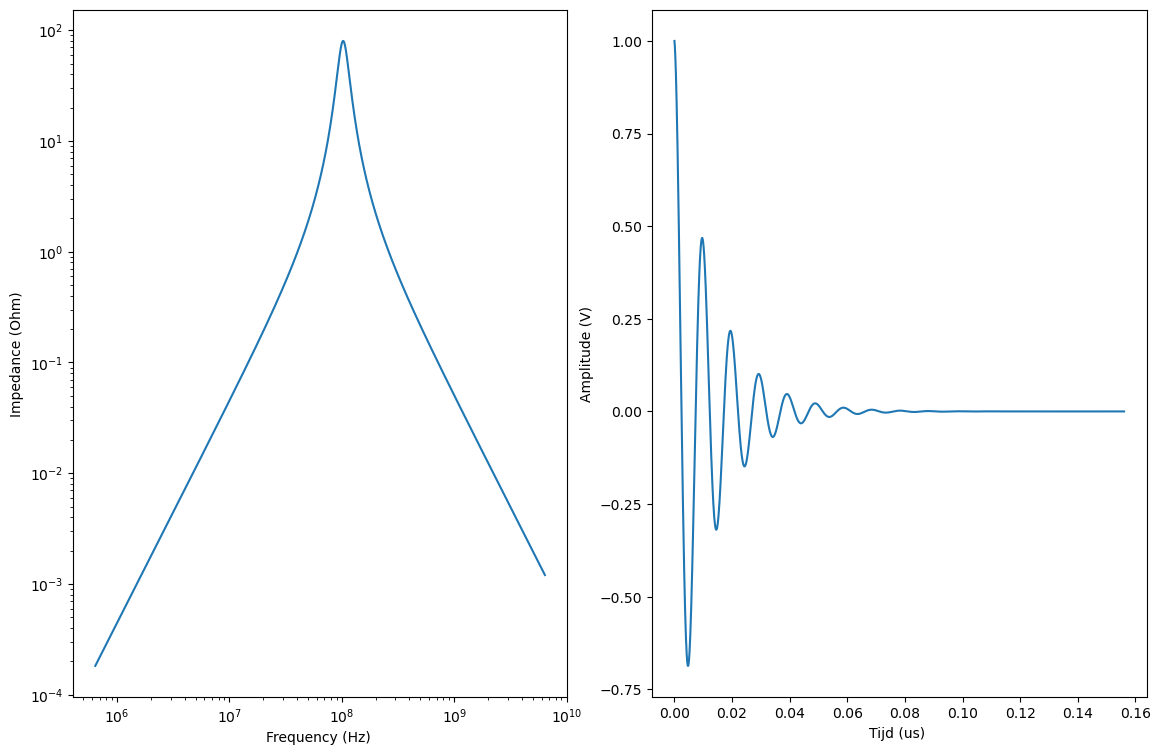
Fig. 23 (links) impedantie van de LRC-kring als functie van de frequentie (rechts) het uitdempen van deze kring als functie van de tijd.

Het is ook zinvol om een simulatie te doen van de amplitude van het signaal als functie van de frequentie van de aansturing. Op het eerste zicht lijkt het .ac commando in SPICE hier de aangeweze methode. Dit is echter niet het geval. Het .ac commando in SPICE doet een klein signaal simulatie, en hierbij wordt aangenomen dat een volledig sinusvormig signaal zich doorheen het circuit beweegt van de ingang naar de uitgang. Dat is voor een klasse C versterker zeker niet het geval. Eigenlijk is het enige werkingsregime waar we een kleinsignaalsimulatie zouden kunnen uitvoeren het instelpunt waarbij \(\alpha=\pi\), met andere woorden de klasse-A modus.

Spice Listing 6 Klasse C circuit AC simulatie

* Class C amp 1
Q_Q1         2 1 0 Q2
L_L1         2 3  1uH  
C_C1         2 3  10n  
R_RL         2 3  60  
V_Vdd        3 0 11V
R_Rin        4 1 100
V_Vin        4 5  AC 0.5V 0 DC 0
V_VinDC      5 0 0.7V
.model Q2  NPN(Is=14.34f BF=200)

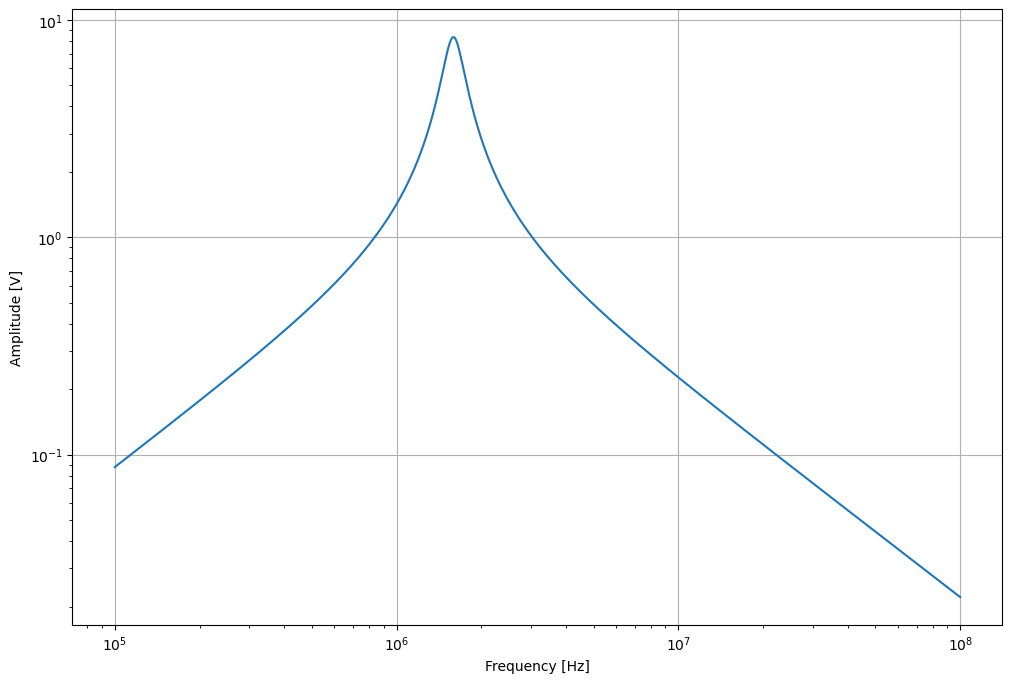
Fig. 24 Amplitude van de spanning op knoop 2 (spice simulatie) als functie van de frequentie van aansturing.

Het is duidelijk uit de bovenstaande figuur dat de amplitude respons van een klasse C versterker is heel gelijkaardig aan de berekende impedantie \(Z(\omega)\) van de trilkring. Dit is ook logisch aangezien

\( V(\omega)=Z(\omega)* I(\omega)\)

en de stroompuls \(I(\omega)\) hetzelfde blijft wanneer de freqentie hetzelfde bij alle frequenties.

Alternatieve berekening van \(V_a\)

In vergelijking (8) werd \(V_a\) berekend op basis van een vermogenevenwicht, namelijk het totale vermogen dat in de trilkring gaat, is ook het totale vermogen dat in de belasting wordt bekomen. Hierbij werd echter verondersteld dat alle vermogen in de eerste harmonische van de trilkring terechtkomt. Dat hoeft natuurlijk niet helemaal het geval te zijn. Een alternatieve berekening voor \(V_a\) is het opsplitsen van de aangelegde stroompulsen in een fourier reeks en elk van de sinusfucties die dan bekomen wordt leggen we dan aan aan de LRC kring. Hierdoor krijgen we de amplitude van alle harmonischen \(V_{a,n}\). Het is natuurlijk wel zo dat de impedantie van de LRC kring off-resonance groot is (zie bovenstaande grafiek), wat maakt dat \(V_{a,n}\) voor \( n > 1\) klein zal zijn.

\[ V_{a,1}= \frac{R_L}{\pi} \int_{-\pi}^{\pi} {\cos(u) I_c(u) du }= \frac{R_L}{\pi} \int_{-\alpha}^{\alpha} {\cos(u) \frac{\cos(u)-\cos(\alpha)}{1-\cos(\alpha)}I_p du }= \frac{I_p R_L}{2\pi}\frac {2 \alpha -\sin(2 \alpha)}{1-\cos(\alpha)} \]

Berekening van de harmonische componenten

\[ V_{a,n}= \frac{Z_L(n \omega_c)}{\pi} \int_{-\pi}^{\pi} {\cos(n u) I_c(u) du }\]

\[ V_{a,n}= \frac{Z_L(n \omega_c)}{\pi} \int_{-\alpha}^{\alpha} {\cos(n u) \frac{\cos(u)-\cos(\alpha)}{1-\cos(\alpha)}I_p du }\]

\[ V_{a,n}=\frac{2 I_p Z_L(n \omega_c)}{\pi} \frac{ \cos (\alpha) \sin ( n \alpha)-n \sin (\alpha) \cos (n \alpha)}{n(n^2-1)(1-\cos(\alpha))}\]

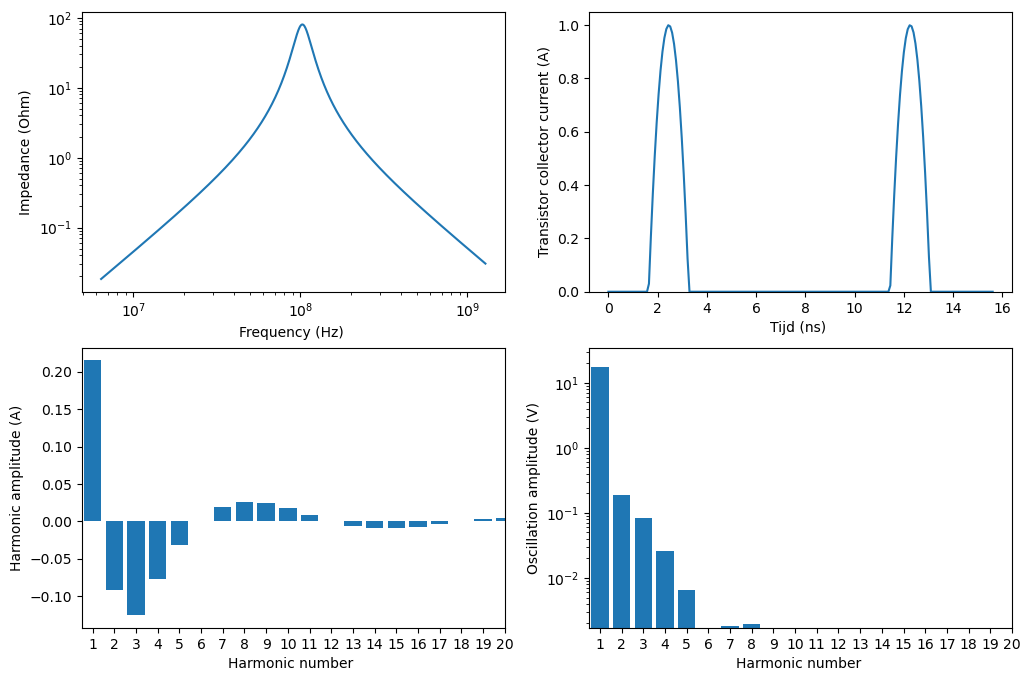
Fig. 25 De contributies van de verschillende harmonischen in het aanstuursignaal en de impact hiervan op de bekomen oscillatie amplitude.

We merken op dat wanneer \(\alpha = 90^o\), we dan geen even harmonischen krijgen. Dat is hetzelfde als bij de klasse B. Ook het rendement is gelijkaardig als de klasse B. Het gebrek aan even harmonischen is relevant voor een aantal toepassingen.

FM modulatie

We kunnen ook dezelfde berekeningsmethode gebruiken om de effecten van off-resonant aan te sturen uit te rekenen, bijvoorbeeld in geval van FM modulatie.

Andere aanstuurvormen dan een sinus: blokgolf en driehoek

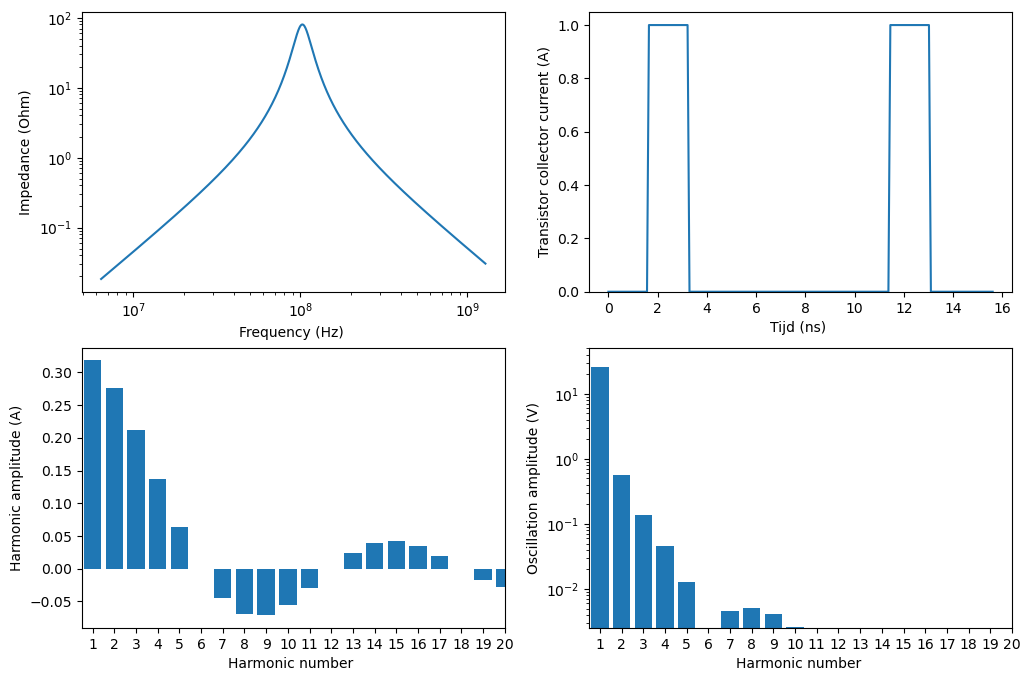
Fig. 26 De contributies van de verschillende harmonischen in een blokgolf aanstuursignaal en de impact hiervan op de bekomen oscillatie amplitude.

Alternatieve schema’s van de klasse C versterker.

Gebruik makende van een transformator

Een van de belangrijke issues met betrekking van het basisschema van de klasse C versterkers is dat de reference van het outputsignaal is de voedingsspanning in plaats van de grond. Een van de opties om de reference van de voeding naar de grond te brengen, is het vervangen van de het spoel door een transformator, want hierdoor kunnen we de referenctiespanning verleggen naar de grond. De figuur hieronder geeft aan hoe dit kan gerealiseerd worden.

Fig. 27 Klasse C versterker met een transformator in de resonante kring.

Gebruik makende van een LC kring aan de ingang

Dit heeft als voordeel dat er geen resitieve verliezen zijn de de \(R_{in}\) weerstand aan de ingang.

Fig. 28 Klasse C versterker met een LC kring aan de ingang van de transistor.

Uitgangsspanning oscillatie rond de grond

Voor een aantal toepassingen is het niet goed dat de AC uitgangspanning een DC offset heeft. We kunnen dit oplossen door het gebuik van de transformator (zie boven) maar ook aan de hand van een extra spoel \(L_2\) en condensator \(C_2\). Het is belangrijk dat de resonantiefrequentie die bepaald wordt door \(L_2\) en \(C_2\) minstens een factor 10 lager is dan de resonantiefrequentie van de versterker.

Fig. 29 Basisschema van de klasse C versterker waarbij de uitgangspanning oscilleert rond de grond.

Wanneer we het bovenstaand circuit simuleren in spice, krijgen we hetvolgende resultaat.

Spice Listing 7 Spice code van de klasse C versterker waarbij de uitgangspanning oscilleert rond de grond

* klasseC   versie2
Q_Q1         2 1 0  Q2
L_L1         0 3    1uH  
C_C1         0 3    10n  
R_R1         0 3    100  
V_V3         4 0    11V
V_V5         1 0    sin(-2 3.09 1591500) DC=-2
C_C2         2 3    100n  
L_L2         2 4    20uH
.model Q2  NPN(Is=14.34f BF=255.9 Rb=100 )

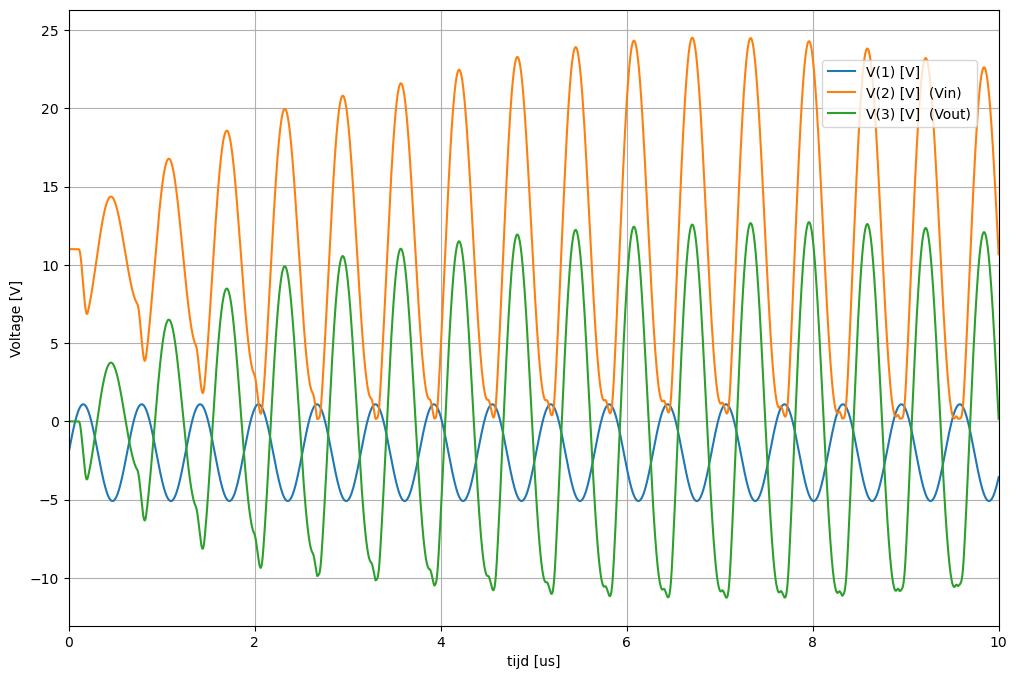
Fig. 30 Resultaat van de spice simulatie van het bovenstaande circuit.

Meerdere versterkingstrappen

In praktijk is het vaak zo dat een klasse C versterker gebruikt wordt om een klein ingangssignaal om te zetten naar een uitgangssignaal dat veel vermogen aan de belasting kan leveren. Vaak is echter een versterkertrap niet voldoende om van het klein ingangssignaal naar het groot uitgangssignaal te gaan, zowel in spanning als in stroom. Om dit te bekomen maken we meestal gebruik van meerdere versterkertrappen.

Hieronder bouwen we stap voor stap op van het hierboven besproken schema naar een schema met 3 achtereenvolgende klasse C versterkerstrappen. Dit schema met 3 versterkerstrappen sluit aan bij een schema dat gebruikt wordt voor mobiele communicatie. Als voorbeeld nemen we [2].

Versterker met 2 Klasse C trappen: stap 1

We vertrekken van het schema van de klasse C versterker zoals gegeven in Fig. 6. We laten in dit schema de belasting \(R_L\) voorlopig eventjes weg. De vergelijking die we hierboven gebruikt hebben om de stroom naar \(C_1\) uit te rekenen is \(I_C= C \frac{d V}{dt}\). We merken op dat deze stroom \(I_C\) niet verandert als we een extra DC spanning over \(C_1\) zetten. We kunnen het schema in Fig. 6 dus aanpassen met een extra spanning over de condensator \(C_1\). Dit levert ons het schema op in Fig. 31.

Fig. 31 Klasse C versterker waarbij de spoel en de condensator aan een verschillende voedingsspanning verbonden zijn.

De werking van dit schema blijft intact gelijk. Als we kijken naar de spanning over \(C_1\) merken we wel op dat er naast een AC spanning ook een DC component van de spanning is. Daardoor neemt de piekspanning toe en zal \(C_1\) sneller doorslagen. We moeten bij de selectie van \(C_1\) dus de keuze maken voor een condensator die een iets hogere spanning aankan. Normaal zal dat betekenen een iets dikker dielectricum en dus een iets hogere prijs.

Versterker met 2 Klasse C trappen: stap 2

Een volgende stap naar een meertraps klasse C versterker is de uitvoering van \(V_{dd2}\) op basis van een spanningsdeling vanuit \(V_{dd}\). Dit schema kan je zien in Fig. 32. Hiervoor gebruiken we de 2 weerstanden \(R_L\) en \(R_{L2}\). Een gevolg hiervan gaat zijn dat de AC-stroom die door de condensator \(C_1\) loopt ook door de weerstanden \(R_L\) of \(R_{L2}\) gaat lopen (i.e. verdeeld proportioneel met de geleidbaarheden van \(R_L\) en \(R_{L2}\)). Hierdoor voeren we terug de belastingsweerstand in die we in de vorige stap weggelaten hebben.

Fig. 32 Een andere versie van bovenstaand schema waarbij \(V_{dd2}\) opgebouwd is aan de hand van een spanningsdeling.

Versterker met 2 Klasse C trappen: stap 3

De belastingsweerstand \(R_{L2}\) kunnen we vervangen door een (voorwaarts gebiaste) diode (\(D_L\)). Dit schema zie je in Fig. 33. Aangezien een voorwaarts gebiaste diode een lage aanweerstand heeft (of dus een hoge geleidbaarheid), zal de meerderheid van de stroom tijdens het voorwaarts gedeelte van de swing door de diode gaan.

Fig. 33 Een andere versie van bovenstaand schema waarbij een diode gebruikt wordt als actieve belasting.

Versterker met 2 Klasse C trappen: stap 4

In een volgende stap versterken we de stroom door de last diode \(D_L\) met een factor \(\beta_F\) van een transistor. De werking blijft hetzelfde, maar in \(R_L\) krijgen we een factor \(\beta_F\) meer stroom. Dit schema zie je in Fig. 34.

Fig. 34 Een andere versie van bovenstaand schema waarbij de diode vervangen is door een transistor.

Versterker met 2 Klasse C trappen: stap 5

De belasting \(R_L\) in Fig. 34 kan nu terug resonant gemaakt worden door het invoeren van de 2de trilkring op basis van \(L_2\) en \(C_2\). We hebben nu een 2-trap klasse C versterker met 2 resonante kringen. Dit schema zie je in in Fig. 35. Het spreek vanzelf dat we hier

\[\frac{1}{L_1 C_1} = \frac{1}{L_2 C_2}\]

moeten kiezen.

Fig. 35 Een andere versie van bovenstaand schema waarbij de tweede transitor belast wordt door een tweede resonante kring aan dezelfde frequentie.

Versterker met 3 Klasse C trappen

Volgens de zelfde redenering kunnen we ook een derde klasse C versterkertrap toevoegen. Dit schema zie je in Fig. 36. Hier geldt:

\[\frac{1}{L_1 C_1} = \frac{1}{L_2 C_2}= \frac{1}{L_3 C_3}\]

Fig. 36 Een andere versie van bovenstaand schema waarbij een derde trap toegevoegd werd aan de versterker.

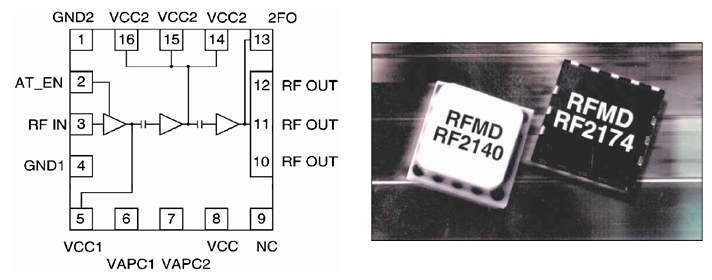
Het circuit in Fig. 36 wordt ook gebruikt in de GSM transmitter ICs RFMD RF2140 en RF2174. Deze ICs werken tussen 1710 en 1785 MHz, gebruiken een voedingsspanning van 3.2V en bekomen en zendvermogen van 32.7 dBm (ongeveer 2 W) met een efficiëntie van 50.6%.

De spoelen (\(L_1\),\(L_2\) en \(L_3\)) en de condensator \(C_3\) worden wel extern uitgevoerd en zitten dus niet in de IC [2].

We herkennen \(L_1\) tussen VCC1 (Pin 5) en \(V_{dd}\), \(L_2\) tussen VCC2 (Pinnen 14,15,en 16) en \(V_{dd}\) en \(L_3\) tussen RF OUT (Pinnen 10,11 en 12) en \(V_{dd}\).

Fig. 37 IC schema en fotos van de RFMD RF2140 en RF2174 [2]

Plaatmodulatie

Wanneer we amplitude modulatie willen bekomen op hoge frequentie, kunnen we dit bekomen door de amplitude aan te passen bij een vaste voedingsspanning. Dit kan door ofwel de amplitude van de stroompulsen (\(I_p\)) aan te passen of door de geleidingshoek (\(\alpha\)) aan te passen.

Echter, zoals we uit de berekeningen van het rendement (\(\eta\)) bij niet-volledige uitsturing en ook uit simulaties zoals bijvoorbeeld aan de hand van widgets kunnen uitgevoerd worden zoals in Fig. 16 kunnen afleiden, is het rendement (\(\eta\)) van een klasse C versterker die niet volledig uitgestuurd wordt tot een amplitude lager dan de voedingsspanning, altijd lager dan wanneer dat wel het geval is. Daarom verkiezen we steeds de klasse C versterker te gebruiken met een amplitude die overeenkomt met de voedingsspanning.

Hoe kunnen we dan die amplitude aanpassen, wel door een klasse B versterker te gebruiken om de voedingsspanning van een klasse C versterker aan te sturen. Dit concept noemen we plaatmodulatie.

Fig. 38 toont schematisch aan hoe zo een plaatmodulatie kan gerealiseerd worden.

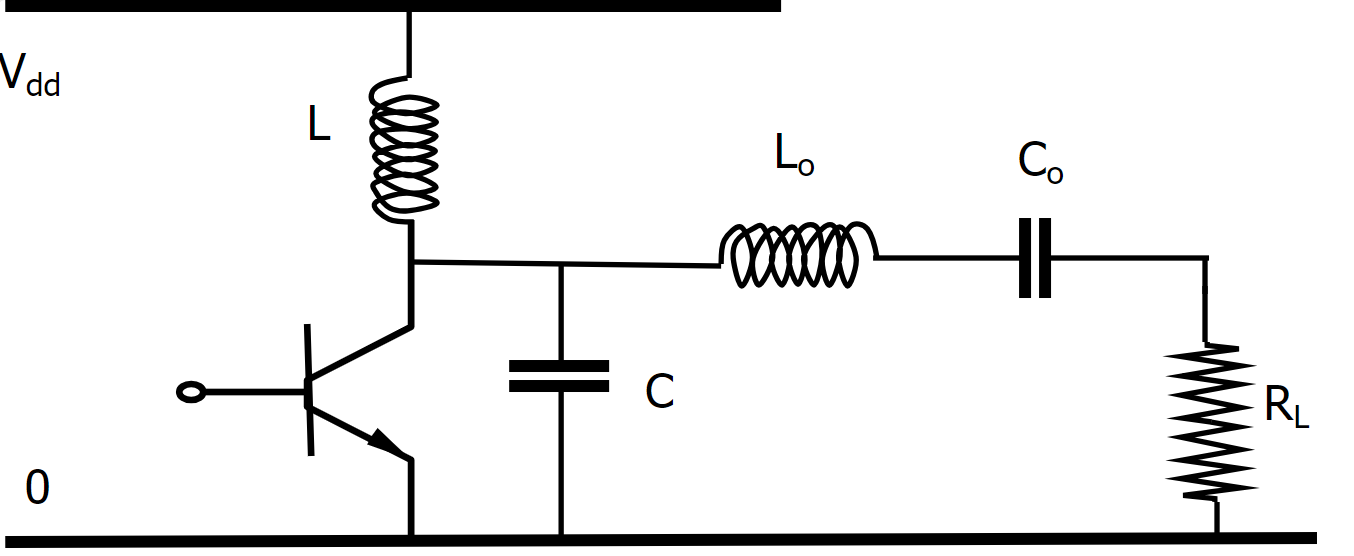
In dit geval levert de voeding (\(V_{dd}\)) het DC vermogen en dus ook de DC stroom die naar de voeding van klasse C versterker gaat. De spoel \(L\) moet dan voldoende groot zijn om deze DC stroom nauwkeurig constant te houden. De klasse B versterker moet dan enkel het vermogen leveren om de veranderingen van voedingsspanningen van de klasse C te kunnen bekomen. De condensator \(C\) moet derhalve ook groot genoeg zijn om snel genoeg de AC stroom te kunnen leveren die de aanpassingen van de voeding mogelijk maakt.

Fig. 38 Amplitude modulatie bekomen door een klasse B versterker te gebruiken om de voeding van de klasse C versterker aan te sturen.

Zelftest via Flashcards

\(\,\!\)

Klik op de vraag als je je antwoord wil nakijken. Klik op next om de volgende vraag te bekomen.