Transmissie lijnen

Figuur 139 toont een overzicht van de verschillende soorten transmissielijnen. Dit omvat zowel coaxiale kabels, golfgeleiders, twisted-pair kabels als baantjes op een PCB. Schematisch zullen we elk van deze transmissielijnen voorstellen als in Figuur 141. Het is belangrijk hierbij te beseffen dat bestaat uit 2 geleiders waartussen een golf zich verplaatst van de bron (generator) naar de belasting (load) (zie Figuur 140).

Figuur 139 Overzicht van de verschillende soorten transmissielijnen

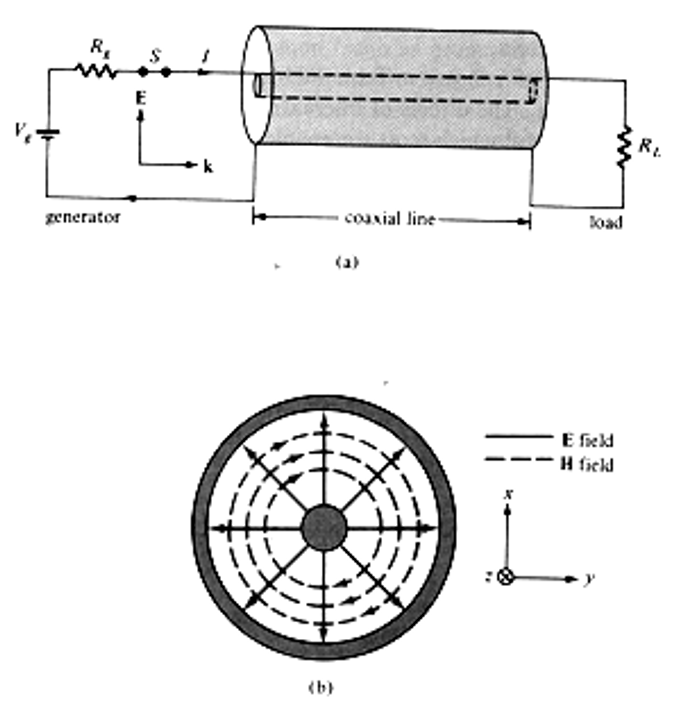
Figuur 140 visuele weergave van het elektrisch (E) en het magnetisch (H) veld in een coax kabel

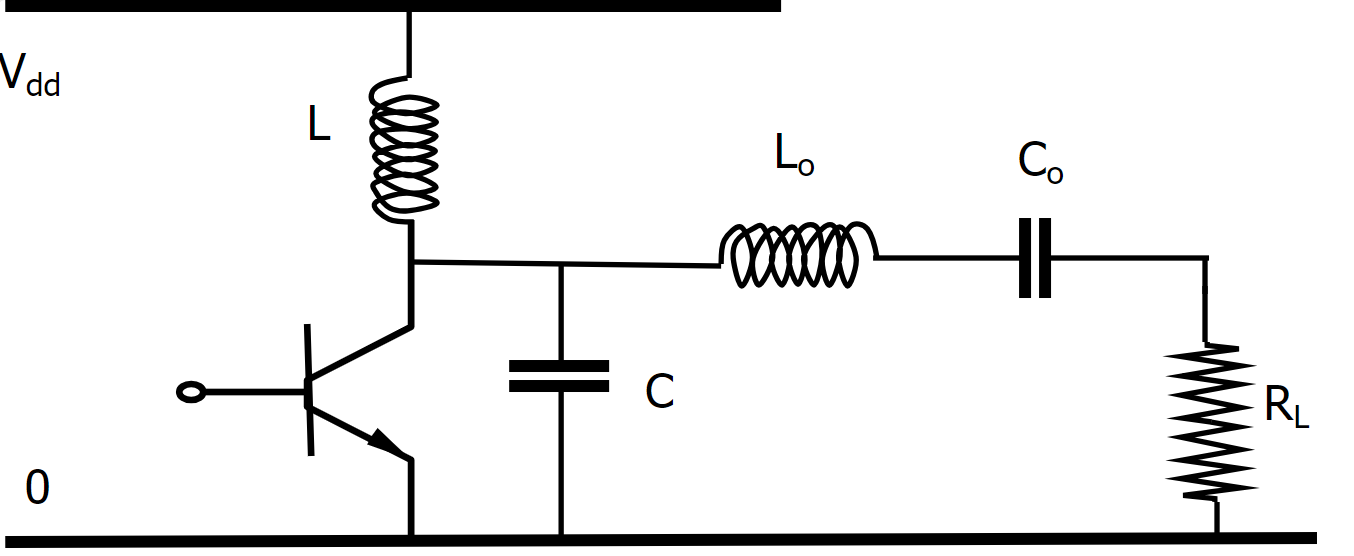
Figuur 141 Netwerk model van een 50 Ohm transmissielijn.

Transmissie lijn model

De golf langs een transmissielijn modelleren we in functie van zowel de plaats (z) als de tijd (t). Het elektrisch veld (E) integreren we tussen de 2 geleiders wat ons de spanning \(v(z,t)\) geeft en het magnetisch veld (H) integreren we over een lus wat ons de stroom door deze lus \(i(z,t)\) geeft. De vergelijkingen voor zowel \(v(z,t)\) als \(i(z,t)\) kunnen we bekomen door een klein stukje van de kabel met lengte \(\Delta z\) te bekijken, zoals getoond in Figuur 142. We hebben spanningsval over de lengte \(\Delta z\) omwille van de spanning over het spoel \(L\) en de weerstand \(R\) van het koper van de geleider, waarbij \(L\) de spoelwaarde is per eenheid afstand en \(R\) de weerstandwaarde per eenheid afstand. Bovendien hebben we ook een stroomverschil over de afstand \(\Delta z\) omwille van het opladen van \(C\) en de lek \(g\), waarbij \(C\) de condensatorwaarde is per eenheid afstand en \(g\) de lekgeleidbaarheid per eenheid afstand. Dit resulteert in het stelsel van vergelijkingen golf.

Figuur 142 Kleinsignaal model van een kort stuk

\[\begin{split}\left\{\begin{matrix} v(z,t)- v(z+ \Delta z) &=L \Delta z \frac {\delta i}{\delta t} + R \Delta z i \\ i(z,t)- i(z+ \Delta z) &=C \Delta z \frac {\delta v}{\delta t} + g \Delta z v \end{matrix}\right.\end{split}\]

\[\begin{split}\left\{\begin{matrix} \frac{v(z,t)- v(z+ \Delta z)}{\Delta z} =L \frac {\delta i}{\delta t} + R i \\ \frac{i(z,t)- i(z+ \Delta z)}{\Delta z} =C \frac {\delta v}{\delta t} + g v \end{matrix}\right.\end{split}\]

z infinitisimaal klein maken:

\[\begin{split}\left\{\begin{matrix} \frac{\delta v}{\delta z} &=L \frac {\delta i}{\delta t} + R i \\ \frac{\delta i}{\delta z} &=C \frac {\delta v}{\delta t} + g v \end{matrix}\right.\end{split}\]

We groeperen van stroom en spanning:

\[\begin{split}\left\{\begin{matrix} \frac{\delta v}{\delta z} &= (j \omega L + R ) i \\ \frac{\delta i}{\delta z} &= (j \omega C + g ) v \end{matrix}\right.\end{split}\]

Beide vergelijkingen combineren geeft:

\[ \frac{\delta v}{\delta i} = \frac{(j \omega L + R ) i}{(j \omega C + g ) v }\]

We groeperen stroom en spanning:

\[ \frac{v \delta v}{i\delta i} = \frac{j \omega L + R }{j \omega C + g }\]

We schrijven het resultaat in de vorm van karakteristieke impedantie:

\[ Z_o^2 = \frac{j \omega L + R }{j \omega C + g }\]

\[ Z_o=\sqrt{\frac{j \omega L+R}{j \omega C+g}}\]

waarbij L de inductantie per eenheid lengte is, C de capaciteit er eenheid lengte is, R de weerstand van de geleider en g de lekgeleidbaarheid van het diëlectricum.

In het beste geval is de weerstand van de geleider nul (R=0) en de lek ook nul (g=0). \(Z_o\) wordt dan

\[ Z_o \approx \sqrt{\frac{L}{C}}\]

Coax kabel

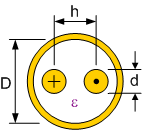
Figuur 143 toont de doorsnede van een coax kabel met daarop de belangrijkste parameters voor het bepalen van de C per eenheid lengte en de L per eenheid lengte.

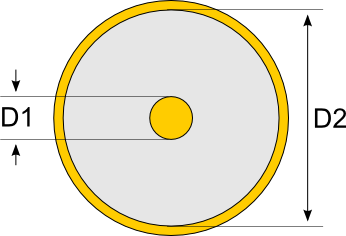
Figuur 143 Schematische cross-section van een coax kabel met de aanduiding van de belangrijkste parameters

Voor een typische coax-kabel met binnendiameter 1.2 mm en buiten diameter 2.8 mm bekomen we de volgende parameters:

R = 0.09886 ohms/m
L = 169.46 nH/m
G = 7.416 S/m
C = 65.63 pF/m
Zo= 50.81 Ohm

Het verloop van de karakteristieke impedantie ziet er voor deze coax kabel uit als aangegeven in Figuur 144

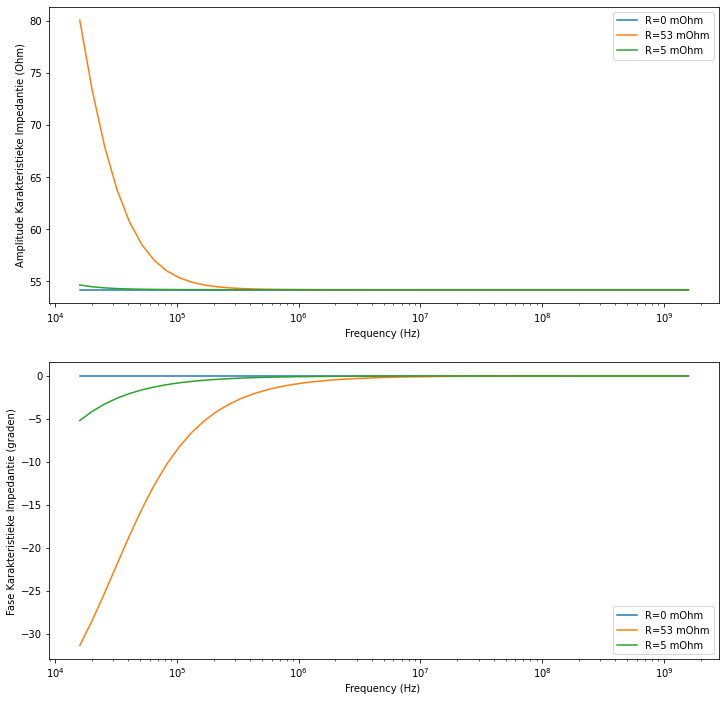
Figuur 144 Verloop van de karakteristieke impedantie van een RG-58 coax als functie van de frequentie.

Uit Figuur 144 merken we dat bij lage frequenties deze karakteristieke impedantie in belangrijke mate verschilt van 50 Ohm. De negatieve fase geeft aan dat bij lage frequenties de lijn zich capacitief gedraagt.

Twisted pair kabel

Figuur 145 toont de doorsnede van een twisted pair kabel met daarop de belangrijkste parameters voor het bepalen van de C per eenheid lengte en de L per eenheid lengte.

Figuur 145 Schematische cross-section van een twisted pair kabel met de aanduiding van de belangrijkste parameters

striplijn

Microstriplijn

De relevante parameters hier zijn de breedte van het baantje (\(w\)) en de dikte van het diëlectricum (\(h\)). Natuurlijk speelt de relatieve Permittiviteit van het diëlectricum (\(\epsilon_r\)) ook mee.

Een voorbeeld:

We willen een 50 Ohm transmissielijn bekomen voor een 2.4 GHz signaal op een PCB waarvan de relatieve Permittiviteit van het diëlectricum \(\epsilon_r\)=4.6. De dikte van het diëlectricum is 1/16 inch

Breedte van het baantje w = 2.931e+00 mm, Rel. perm: e_eff = 3.460
Breedte van het baantje  w = 1.154e+02 mils (vaak voorkomende PCB eenheid)
-----------------------------------------------------
Weerstand per eenheid lengte: R' = 0 ohms/m
Inductantie per eenheid lengte: L' = 3.100e+02 nH/m
lek geleidbaarheid per eenheid lengte: G' = 0 S/n
Capaciteit per eenheid lengte: C' = 1.240e+02 pF/m
-----------------------------------------------------
Golflengte in de vrije ruimte: lambda = 1.250e+01 cm
Golflengte in het medium (guide): lambda_g = 6.720e+00 cm

Quart golflengte bij 2.4 GHz  = 1.680 cm

Breedte van het baantje w = 1.884e+00 mm, Rel. perm: e_eff = 3.338
Breedte van het baantje  w = 7.418e+01 mils (vaak voorkomende PCB eenheid)
-----------------------------------------------------
Weerstand per eenheid lengte: R' = 0 ohms/m
Inductantie per eenheid lengte: L' = 3.898e+02 nH/m
lek geleidbaarheid per eenheid lengte: G' = 0 S/n
Capaciteit per eenheid lengte: C' = 9.516e+01 pF/m
-----------------------------------------------------
Golflengte in de vrije ruimte: lambda = 6.000e+01 cm
Golflengte in het medium (guide): lambda_g = 3.284e+01 cm

Microstrip Analyse Plots

We vergelijken 3 types: Micro-fiber PTFE, FR4, en Ceramisch-gevulde PTFE voor een aantal waardes van \(w/h\).

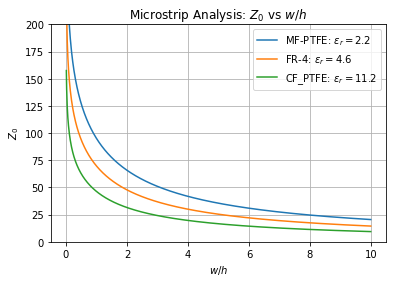
Figuur 146 Verloop van de karakteristieke impedantie van een microstriplijn als functie van de dimensies.

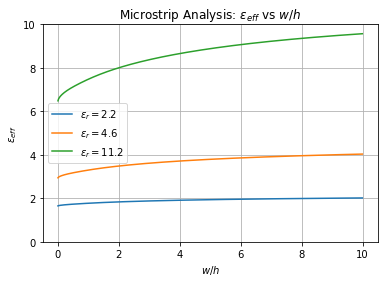
Figuur 147 Verloop van de dielectrische constante van een microstriplijn als functie van de dimmensies.

Microstrip Design Plots

Voor het design doen we eigenlijk het omgekeerde van de analyse: we vertrekken van een gevraagde \(Z_o\) en we rekenen uit wat de \(w\) en \(h\) moeten zijn om dit te bekomen. We vergelijken 3 types: Micro-fiber PTFE, FR4, en Ceramisch-gevulde PTFE voor een aantal waardes van \(w/h\).

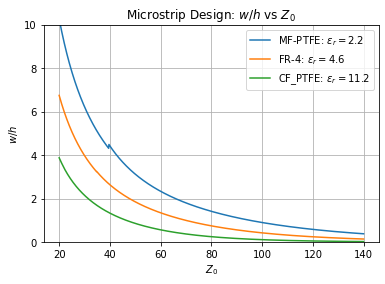
Figuur 148 Dimensies om de vereiste karakteristieke impedantie van een microstriplijn te bekomen.

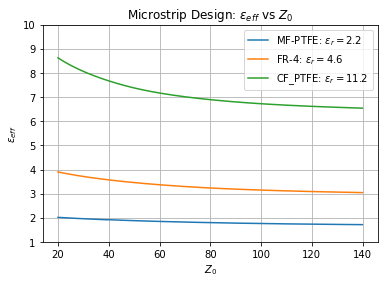
Figuur 149 De relatie tussen effectieve dielectrische constante en karakteristieke impedantie.

Andere transmissie lijnconfiguraties

Twee geleiders in een onbeperkt medium

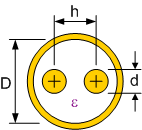
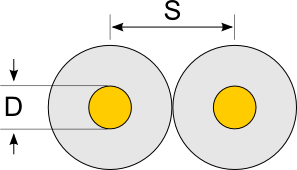
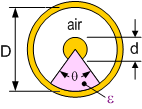
Figuur 150 toont de doorsnede van 2 gelijke geleiders met diameter \(d\) op een afstand \(D\) van elkaar verwijderd. De karakteristieke impedantie \(Z_0\) van deze topologie is:

\[Z_0= \frac{1}{\pi}\sqrt{\frac{\mu}{\epsilon}}\cosh^{-1}\left(\frac{D}{d}\right) \approx \frac{119.92}{\sqrt{\epsilon}} \ln\left(\frac{2D}{d}\right) \approx \frac{276}{\sqrt{\epsilon}} \log_{10}\left(\frac{2D}{d}\right)\]

Voor de geldigheid van deze formule is het essentieel dat beide geleiders een gelijke en tegengestelde stroom geleiden.

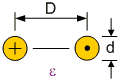
Figuur 150 Twee geleiders in een onbeperkt medium

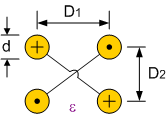
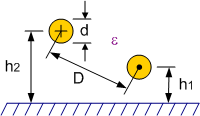
Het is ook mogelijk dat beide geleiders niet dezelfde diameter hebben. In Figuur 151 wordt de doorsnede geschetst voor de diameters \(d_1\) en \(d_2\).

De karakteristieke impedantie \(Z_0\) van deze topologie is:

\[Z_0= \frac{1}{2\pi}\sqrt{\frac{\mu}{\epsilon}}\cosh^{-1}\left(\frac{1}{2}\left(\frac{4 D^2}{d_1 d_2} -\frac{d_1}{d_2}-\frac{d_2}{d_1}\right)\right) \]

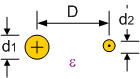
Figuur 151 Doorsnede van een transmissielijn met 2 geleiders van ongelijke diameters.

Een geleider boven een grondvlak

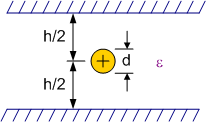
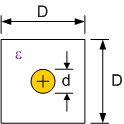
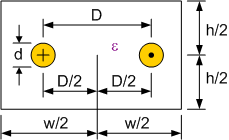
Figuur 152 toont de configuratie van een geleider boven een grondvlak. Hierbij is het vanzelfsprekend dat de terugstroom door het grondvlak loopt. Daarom wordt de waarde van de karakteristieke impedantie \(Z_0\) bekomen tussen deze geleider en het grondvlak.

\[Z_0= \frac{138}{\sqrt{ε}} \log_{10}\left(\frac{4h}{d}\right) \]

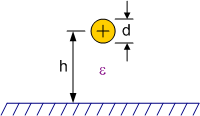
Figuur 152 configuratie van een geleider boven een grondvlak

Twee geleiders boven een grondvlak

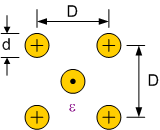
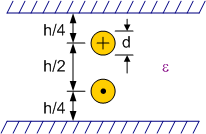
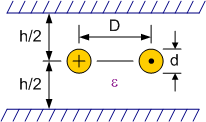
Hierbij is het belangrijk dat we het verschil beschouwen tussen de differentiële karakteristieke impedantie (zie Figuur 153) en de common mode karakteristieke impedantie (zie Figuur 154).

Wanneer d << D en d << h worden de vergelijkingen:

\[Z_{0_{diff}}= \frac{276}{\sqrt{ε}} \log_{10}\left(\frac{2D}{d}\frac{1}{\sqrt{1+\left(\frac{D}{2h}\right)^2}}\right) \]

\[Z_{0_{common}}= \frac{69}{\sqrt{ε}} \log_{10}\left(\frac{4h}{d}\frac{1}{\sqrt{1+\left(\frac{2h}{D}\right)^2}}\right) \]

We zien ook dat als \(D\) zeer groot wordt, de waarde van \(Z_{0_{common}}\) de helft wordt van de waarde van een enkelvoudige geleider boven een grondvlak, met andere woorden: voor grote D kunnen we beide geleiders in parallel beschouwen.

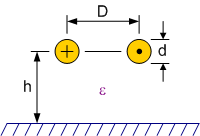
Figuur 153 differentiele karakteristieke impedantie boven een grondvlak

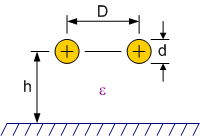
Figuur 154 common mode karakteristieke impedantie boven een grondvlak