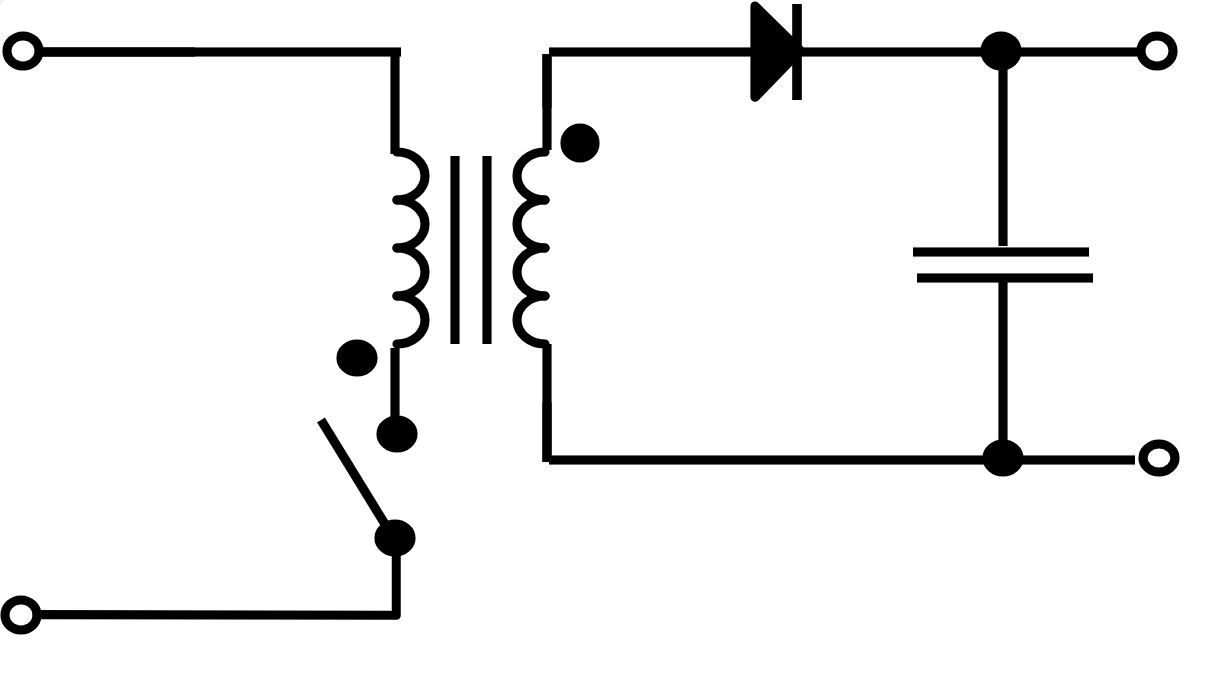
Boost Converter of Step-up Converter

De relatie tussen de Duty cycle (\(D\)) en de uitgangsspanning (\(V_{uit}\)) voor een gegeven ingangsspanning (\(V_{in}\)) kunnen we het best bereken vanuit het perspectief van de stroomverandering door het spoel. Inderdaad, de spanning over het spoel is evenredig met de stroomstijging per tijdseenheid.

\[ U_L= L \frac{dI}{dt} \]

Hieruit volgt dat tijdens de tijd dat de transistor aan staat \((T_{on})\):

\[ U_L= L \frac{\Delta I}{T_{on}} \]

en tijdens de tijd dat de transistor af staat \((T_{off})\):

\[ U_L= L \frac{-\Delta I}{T_{off}} \]

We vullen dit in en we bekomen:

\[ U_L= L \frac{\Delta I}{T_{on}} = \]

\[ U_L= - L \frac{\Delta I}{T_{off}} = \]

met ** zijnde ***. Uit beide vergelijkingen kunnen we nu \(L \Delta I \) extraheren en deze 2 waardes aan elkaar gelijkstellen. Dit geeft:

\[ L \Delta I = T_{on}() =-T_{off}() \]

---

Wanneer we deze vergelijking nu oplossen naar \(V_{uit}\) en de stroom door het spoel \(I_L\) bekomen we:

\[ V_{uit}= \frac{1}{1-D}V_{in} -V_D-\frac{1}{1-D}R_L I_{L}-\frac{D }{1-D} R_T I_{L}\]

In de meeste gevallen willen we echter de uitgangsspanning als functie van een gegeven uitgangsstroom \(I_{out}\).

\[ V_{uit}= \frac{1}{1-D}V_{in} -V_D-\frac{1}{(1-D)^2}R_L I_{out}-\frac{D }{(1-D)^2} R_T I_{out}\]

We kunnen de vergelijking ook schrijven in functie van de duty cycle \(D\). We zien dat er hier 2 oplossingen zijn.

Fig. 87 Visualisatie van de werking van de boost convertor