Berekening van elektronische circuits

In dit hoofdstuk bespreken we de wijze waarop complexe circuits uitgerekend worden.

De Modified Nodal Analysis

De Modified Nodal Analysis (MNA) methode werd voor het eerst geïntroduceerd door [1] in 1975.

De stempel van een weerstand in een MNA matrix

Fig. 16 weerstand met labels voor MNA matrix

De uitgaande stroom van knoop \(i\) is:

(1)\[\begin{equation}\label{eq:cond} I_{ij}=g (V_i-V_j) = g V_i - g V_j, \end{equation}\]

waarbij \(g= \frac{1}{R}\) de conductiviteit is van de weerstand \(R\).

Op eenzelfde manier kunnen we opschrijven dat de uitgaande stroom van knoop \(j\) is:

(2)\[\begin{equation}\label{eq:cond2} I_{ji}=-I_{ij}=g (V_j-V_i) = -g V_i + g V_j \end{equation}\]

De stroomwet van Kirchoff geeft aan dat de som van alle stromen uitgaande van knoop \(i\) nul is.

(3)\[\begin{equation}\label{eq:Kirchoff} \sum_{j \neq i}^n I_{ij}=0. \end{equation}\]

Eenzelfde vergelijking kunnen we voor elke van de \(n\) knopen in het circuit opstellen. In matrix notatie wordt dat:

(4)\[\begin{equation}\label{eq:MatrixR1} \begin{bmatrix}\vdots & & \vdots & & \vdots \\ \dots & g & \dots & -g & \dots \\ \vdots & & \vdots & & \vdots \\ \dots & -g & \dots & g & \dots \\ \vdots & & \vdots & & \vdots \end{bmatrix} \begin{bmatrix} \vdots \\ V_i \\ \vdots \\ V_j \\ \vdots \end{bmatrix} =\begin{bmatrix} \vdots \\ 0 \\ \vdots \\ 0 \\ \vdots \end{bmatrix} \end{equation}\]

Als alternatief voor deze stempel van de weerstand op basis van de conductiviteit \(g\) kunnen we overwegen om een bijkomende onbekende \(I_{ij}\) en een bijkomende vergelijking in te voegen

(5)\[\begin{equation}\label{eq:cond3} V_i-V_j - R I_{ij} = 0. \end{equation}\]

Op de vergelijkingen van knoop i en j voegen we dan telkens ook \(I_{ij}\) of \(-I_{ij}\) toe. De MNA matrix wordt dan:

(6)\[\begin{equation}\label{eq:MatrixR2} \begin{bmatrix}\vdots & & \vdots & & \vdots & & \vdots \\ \dots & & \dots & & \dots & 1 & \dots \\ \vdots & & \vdots & & \vdots & & \vdots \\ \dots & & \dots & & \dots & -1 & \dots \\ \vdots & & \vdots & & \vdots & & \vdots \\ \dots & 1 & \dots & -1 & \dots & -R & \dots \\ \vdots & & \vdots & & \vdots & & \vdots \end{bmatrix} \begin{bmatrix} \vdots \\ V_i \\ \vdots \\ V_j \\ \vdots \\ I_{ij} \\ \vdots \end{bmatrix} =\begin{bmatrix} \vdots \\ 0 \\ \vdots \\ 0 \\ \vdots \\ 0 \\ \vdots \end{bmatrix} \end{equation}\]

Over het algemeen is het toevoegen van een bijkomende onbekende geen goed idee omdat de grootte van de matrix hierdoor toeneemt en de rekentijd voor matrixinversie kwadratisch toeneemt met de grootte van de matrix. In het geval de weerstand \(R\) heel erg klein wordt, en dus de conductiviteit \(g\) heel erg groot, kan dit wel soms een beter resultaat opleveren.

De stempel van een condensator in een MNA matrix

Fig. 17 Condensator schema

Wanneer er in een circuit een condensator staat tussen knoop \(i\) en knoop \(j\), is de stroom die van knoop \(i\) naar knoop \(j\) loopt

(7)\[\begin{equation}\label{eq:ccc} j\omega C (V_i-V_j) = j\omega C V_i - j\omega C V_j, \end{equation}\]

en de stroom van knoop \(j\) naar knoop \(i\) loopt in de omgekeerde richting. In matrix notatie wordt dat:

(8)\[\begin{equation}\label{eq:MatrixC} \begin{bmatrix}\vdots & & \vdots & & \vdots \\ \dots & j\omega C & \dots & -j\omega C & \dots\\ \vdots & & \vdots & & \vdots \\ \dots & -j\omega C & \dots & j\omega C & \dots \\ \vdots & & \vdots & & \vdots \end{bmatrix} \begin{bmatrix} \vdots \\ V_i \\ \vdots \\ V_j \\ \vdots \end{bmatrix} =\begin{bmatrix} \vdots \\ 0 \\ \vdots \\ 0 \\ \vdots \end{bmatrix} \end{equation}\]

De stempel van een spoel in een MNA matrix

Wanneer er in een circuit een condensator staat tussen knoop \(i\) en knoop \(j\), is de stroom die van knoop \(i\) naar knoop \(j\) loopt

(9)\[\begin{equation}\label{eq:cL} \frac{1}{j\omega L} (V_i-V_j) = \frac{1}{j\omega L} V_i - \frac{1}{j\omega L} V_j, \end{equation}\]

en de stroom van knoop \(j\) naar knoop \(i\) loopt in de omgekeerde richting. In matrix notatie wordt dat:

(10)\[\begin{equation}\label{eq:Matrixspoel} \begin{bmatrix}\vdots & & \vdots & & \vdots \\ \dots & \frac{1}{j\omega L} & \dots & -\frac{1}{j\omega L} & \dots\\ \vdots & & \vdots & & \vdots \\ \dots & -\frac{1}{j\omega L} & \dots & \frac{1}{j\omega L} & \dots \\ \vdots & & \vdots & & \vdots \end{bmatrix} \begin{bmatrix} \vdots \\ V_i \\ \vdots \\ V_j \\ \vdots \end{bmatrix} =\begin{bmatrix} \vdots \\ 0 \\ \vdots \\ 0 \\ \vdots \end{bmatrix} \end{equation}\]

De stempel van een transconductantie in een MNA matrix

Bij een transconductantie wordt de waarde van de stroom van de knoop \(k\) naar de knoop \(l\) bepaalt door de spanning tussen de knoop \(i\) en de knoop \(j\), aan de hand van de vergelijking

(11)\[\begin{equation}\label{eq:gm} I_{kl}= g_m (V_i-V_j) , \end{equation}\]

waarbij \(g_m\) de waarde van de transconductantie is. In matrix notatie wordt dat:

(12)\[\begin{equation}\label{eq:Matrixgm} \begin{bmatrix}\vdots & & \vdots & & \vdots & & \vdots & & \vdots \\ \dots & & \dots & & \dots & & \dots & & \dots\\ \vdots & & \vdots & & \vdots & & \vdots & & \vdots\\ \dots & & \dots & & \dots & & \dots & & \dots\\ \vdots & & \vdots & & \vdots & & \vdots & & \vdots\\ \dots & g_m & \dots & -g_m & \dots & & \dots & & \dots\\ \vdots & & \vdots & & \vdots & & \vdots & & \vdots\\ \dots & -g_m & \dots & g_m & \dots & & \dots & & \dots\\ \vdots & & \vdots & & \vdots & & \vdots & & \vdots \end{bmatrix} \begin{bmatrix} \vdots\\ V_i\\ \vdots \\ V_j\\ \vdots\\ V_k\\ \vdots \\ V_l\\ \vdots \end{bmatrix} =\begin{bmatrix} \vdots\\ 0 \\ \vdots \\ 0 \\ \vdots\\ 0 \\ \vdots \\ 0 \\ \vdots \end{bmatrix} \end{equation}\]

We merken hierin op dat deze matrix nu niet langer symmetrisch is.

In het geval van een MOS transistor zullen we de transcondutantie gebruiken om de \(I_{DS}\) in de simulator in te brengen. In dit geval is de knoop \(j\) en \(l\) dezelfde knoop en komen we tot de vergelijking

(13)\[\begin{equation}\label{eq:gm2} I_{DS}= g_m (V_G-V_S) . \end{equation}\]

In matrix notatie wordt dat:

(14)\[\begin{equation}\label{eq:MatrixMOS} \begin{bmatrix}\vdots & & \vdots & & \vdots & & \vdots \\ \dots & & \dots & & \dots & & \dots \\ \vdots & & \vdots & & \vdots & & \vdots \\ \dots & g_m & \dots & & \dots & -g_m & \dots \\ \vdots & & \vdots & & \vdots & & \vdots \\ \dots & -g_m & \dots & & \dots & g_m & \dots \\ \vdots & & \vdots & & \vdots & & \vdots \end{bmatrix} \begin{bmatrix} \vdots\\ V_G\\ \vdots \\ V_D\\ \vdots \\ V_S\\ \vdots \end{bmatrix} =\begin{bmatrix} \vdots\\ 0 \\ \vdots \\ 0 \\ \vdots \\ 0 \\ \vdots \end{bmatrix} \end{equation}\]

De stempel van een niet-ideale spanningsbron

Een niet-ideale spanningsbron bestaat uit een ideale spanningsbron in serie met de bronweerstand, zoals aangegeven in de linkerkant van Fig. 18.

Fig. 18 (links) Thevenin schema van een niet-ideale spanningsbron (rechts) het overeenkomende Norton equivalent

Voor de berekening aan de hand van een MNA matrix is het handig om dit Thevenin schema om te werken naar zijn Norton equivalent zoals aangegeven aan de rechterkant van Fig. 18. Hierbij is berekenen we de kortsluitstroom \(I_{sc}\) in functie van de open klemmen spanning \(V_{oc}\) en de outputweerstand \(R_o\) van de bron als

(15)\[\begin{equation} I_{sc}=\frac{V_{oc}}{R_o}. \end{equation}\]

In de MNA matrix brengen we de uitgangsconductiviteit \(g_o\) in als

(16)\[\begin{equation} g_o=\frac{1}{R_o}. \end{equation}\]

Het Norton equivalent kunnen we inbrengen in een MNA matrix zonder dat een bijkomende vergelijking nodig is. Dit wordt dan

(17)\[\begin{equation}\label{eq:Norton} \begin{bmatrix}\vdots & & \vdots & & \vdots \\ \dots & g & \dots & -g & \dots \\ \vdots & & \vdots & & \vdots \\ \dots & -g & \dots & g & \dots \\ \vdots & & \vdots & & \vdots \end{bmatrix} \begin{bmatrix} \vdots \\ V_i \\ \vdots \\ V_j \\ \vdots \end{bmatrix} =\begin{bmatrix} \vdots \\ I_{sc} \\ \vdots \\ -I_{sc} \\ \vdots \end{bmatrix} \end{equation}\]

De stempel van een ideale spanningsbron

Fig. 19 Schema van een ideale spanningsbron

In het geval van een ideale spanningsbron of een bijna ideale spanningsbron wordt de outputweerstand \(R_o=0\) ofwel zeer klein. Als een gevolg hiervan wordt de uitgangsconductiviteit \(g_o=\infty\) of zeer groot. De oplossing van de MNA matrix is als gevolg hiervan onbepaald of numeriek erg onstabiel. We kunnen dit voorkomen door een bijkomende onbekenden \(I_{sc}\) en een bijkomende vergelijking in te voeren.

(18)\[\begin{equation} V_i-V_j=V_{oc}. \end{equation}\]

De nieuwe MNA matrix wordt dan

(19)\[\begin{equation}\label{eq:bron} \begin{bmatrix}\vdots & & & & & \vdots & & & \vdots \\ \dots & & & & & \dots & 1 & & \dots \\ \dots & & & & & \dots & -1 & & \dots \\ \vdots & & & & & \vdots & & & \vdots \\ \dots & 1 & -1& & & \dots & \dots & & \dots\\ \vdots & & & & & \vdots & & & \vdots\end{bmatrix} \begin{bmatrix} \vdots\\ V_i\\ V_j\\ \vdots\\ I_{sc}\\ \vdots\end{bmatrix} =\begin{bmatrix} \vdots\\ 0\\ 0\\ \vdots \\ V_{oc}\\ \vdots \end{bmatrix} \end{equation}\]

De stempel van een transformator in een MNA matrix

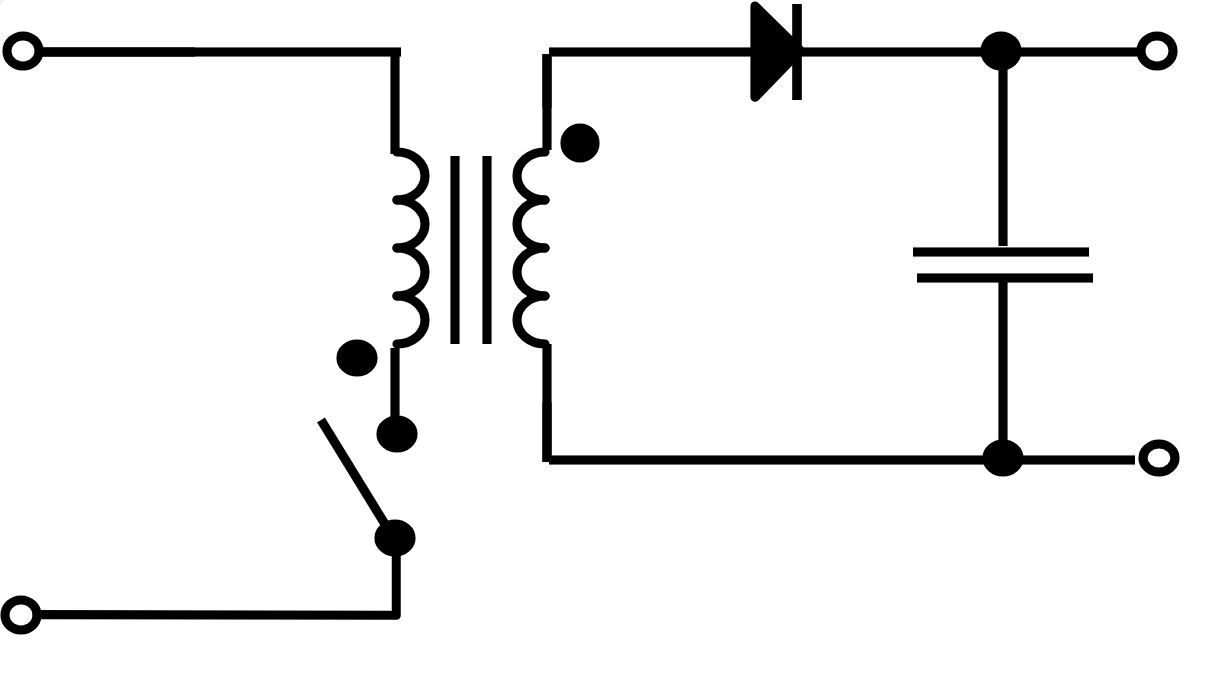
Een transformator met primaire wikkeling \(L_{ij}\) tussen knoop \(i\) en knoop \(j\) en zijn secundaire wikkeling \(L_{kl}\) tussen knoop \(k\) en \(l\) kunnen we voorstellen als in xxx. \(M\) is de koppeling tussen beide spoelen \(L_{ij}\) en \(L_{kl}\).

De vergelijkingen die deze transformator beschrijven zijn dan:

(20)\[\begin{equation}\label{TransformEq} \begin{aligned} V_i-V_j - j \omega L_{ij} I_1 - j \omega M I_2 = 0 \\ V_k-V_l - j \omega M I_1 - j \omega L_{kl} I_2 = 0 \\ \end{aligned} \end{equation}\]

De 2 vergelijkingen TransformEq beschrijven de 2 bijkomende rijen in de MNA matrix. we hebben ook 2 bijkomende onbekenden, namelijk in dit geval de stromen \(I_1\) en \(I_2\) die lopen in de richting van de transformator. Dit wil zeggen dat de stroom \(I_1\) van knoop \(i\) wegloopt en naar knoop \(j\) loopt en dat de stroom \(I_2\) van knoop \(k\) wegloopt en naar knoop \(l\) loopt. Dit bepaalt dan ook de tekens van 1 in de kolommen van respectievelijk \(I_1\) en \(I_2\).

(21)\[\begin{equation}\label{Transformmatrix} \begin{bmatrix}\vdots & & & & & \vdots & & & \vdots \\ \dots & & & & & \dots & 1 & & \dots \\ \dots & & & & & \dots & -1 & & \dots \\ \dots & & & & & \dots & & 1 & \dots \\ \dots & & & & & \dots & & -1 & \dots \\ \vdots & & & & & \vdots & & & \vdots \\ \dots & 1 & -1& & & \dots & - j \omega L_{ij} & - j \omega M & \dots\\ \dots & & & 1 & -1& \dots & - j \omega M & - j \omega L_{kl} & \dots \\ \vdots & & & & & \vdots & & & \vdots\end{bmatrix} \begin{bmatrix} \vdots\\ V_i\\ V_j\\ V_k\\ V_l\\ \vdots\\ I_1\\ I_2\\ \vdots\end{bmatrix} =\begin{bmatrix} \vdots\\ 0\\ 0\\ 0\\ 0\\ \vdots \\ 0\\ 0\\ \vdots \end{bmatrix} \end{equation}\]

We kunnen ons afvragen of het ook hier niet voordelig is eerst het stelsel TransformEq op te lossen zodat we \(I_1\) en \(I_2\) bekomen in functie van \(V_i-V_j\) en \(V_k-V_l\), en dan deze bekomen numerieke waardes invullen in de vergelijkingen met nummer \(i\),\(j\),\(k\),\(l\). Hierdoor hebben we 2 vergelijkingen en 2 onbekenden minder in Transformmatrix. Echter in vele gevallen willen we gebruik maken van een goede transformator en gaat \(M \approx \sqrt{L_{ij} L_{kl}}\) waardoor de determinant \(D\) van dit stelsel \(\approx 0\). Hierdoor wordt het overblijvende stelsel numeriek minder stabiel.