Uitgewerkt voorbeeld van een klasse AB met MOS transistors#
In [4] wordt de klasse AB werking getoond aan de hand van het schema in Fig. 82. We bestuderen dit schema in meer detail. Eerst bekijken we de voorinsteltak. De 2 weerstanden R, samen met de 2 diodes zorgen ervoor dat zonder aangelegd signaal de spanning \(V_i\) gelegen is midden de 2 voedingsspanningen. De 2 weerstanden R zijn dan zo gekozen dat de \(I_B\) een DC stroomcomponenten heeft die mooi kan ingesteld worden door R.
Wanneer we vervolgens een AC signaal aanleggen, krijgen we de volgende signalen:
\(V_I+V_D\) aan de ingang van de nMOS transistor \(M_N\)
\(V_I-V_D\) aan de ingang van de pMOS transistor \(M_P\)
Onder zo goed als alle omstandigheden zullen zowel de nMOS als de pMOS in saturatie zijn. Dit wil zeggen dat de stromen door deze transistors voldoen aan de vergelijkingen:
als \(V_{GSn} >V_{Tn}\)
als \(V_{GSp} <V_{Tp}\)
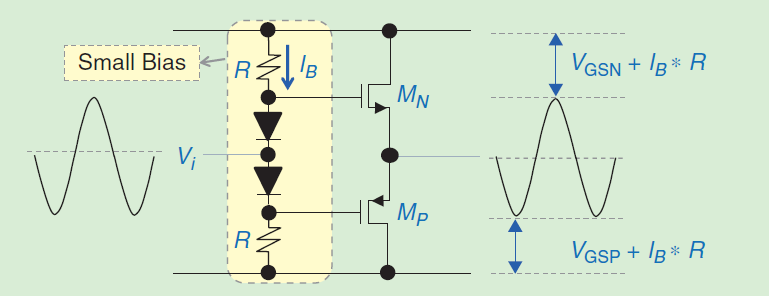
Fig. 82 Klasse AB versterker met MOS transistors#
Wanneer we de spanning aan de gate en de source invullen krijgen we:
\( I_n=\mu_n C_{ox} \frac{W_n}{2L_n} (V_I+V_D- V_{out} -V_{Tn})^2\) als \(V_I+V_D- V_{out} >V_{Tn}\)
\( I_p=\mu_p C_{ox} \frac{W_p}{2L_p} (V_I-V_D -V_{out}-V_{Tp})^2\) als \(V_I-V_D -V_{out} <V_{Tp}\)
\( V_{out}= (I_n -I_p)R_L\)
In Fig. 83 berekenen we deze stromen. We veronderstellen hierbij dat: \(\mu_n C_{ox} \frac{W_n}{2L_n}=\mu_p C_{ox} \frac{W_p}{2L_p}=0.02 A/V^2\),\(V_D=0.7V\), \(V_{Tn}=0.3V\) \(V_{Tp}=-0.3V\) en \(R_L=80 \Omega\).
In Fig. 84 zoemen we in op een detail rond de oorsprong.
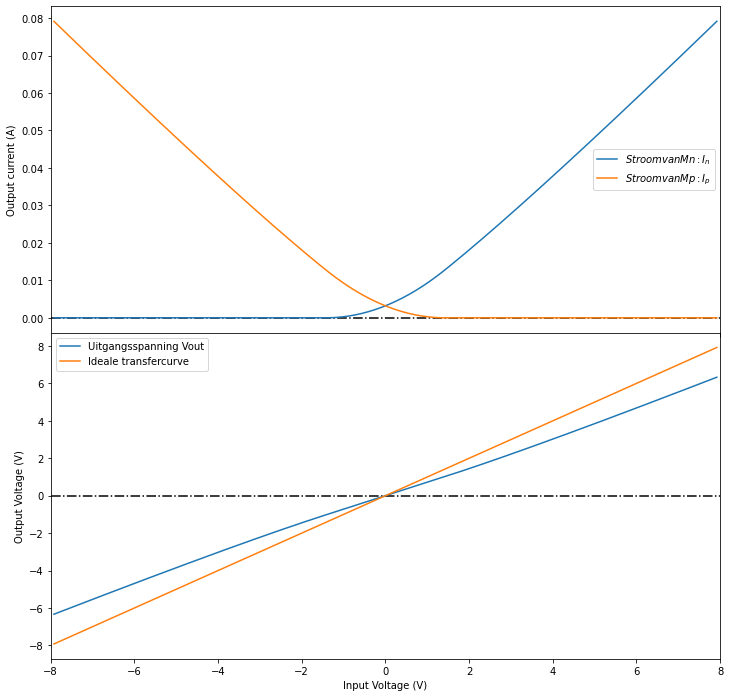
Fig. 83 Transfer curve en stroom van de beide transistors.#
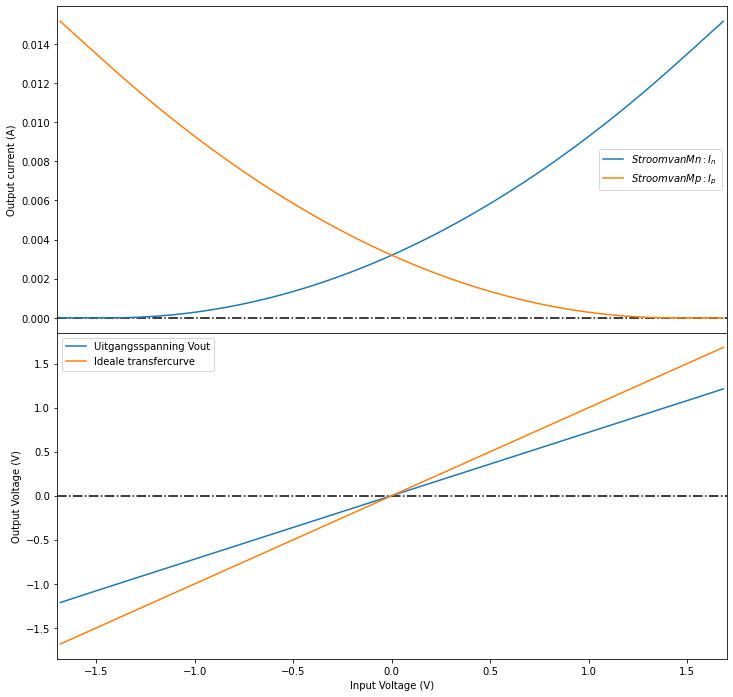
Fig. 84 Detail van de zone rond de oorsprong. We zien dat hier beide transistors in geleiding zijn.#